WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Raaklijn aan grafiek functie f(x)=4sin³x

Hoi,
De volgende som kom ik niet uit, ik zal laten zien wat ik gedaan heb en ik hoop dat jullie me kunnen helpen.
De functie is: f(x)= 4 sin³ x
Ik moet nu de formule opstellen van de raaklijn in het punt A met xA=1/4$\pi$
Ik heb toen eerst de afgeleide bepaald van de formule, dat vond ik al lastig met die sin³. Dus heb ik eerst de formule veranderd in: f(x)=4sinx · sin²x Daarvan heb ik vervolgens de afgeleide bepaald:
f'(x)=4cosx·sin²x + 4sinx·(sinx·cosx+sinx·cosx)
Invullen van x=1/4$\pi$ geeft:
f'(1/4$\pi$)=3√2
De richtingscoëfficient is dus 3√2
De formule van de raaklijn wordt dan k(x)=3√2x+b
Om b te kunnen berekenen moet je de y-coördinaat van het punt weten. Ik kwam uit op:
f(1/4$\pi$)= √2
Dat heb ik ingevuld en toen kwam ik er helemaal niet meer uit:
k(1/4$\pi$)=3√2·1/4$\pi$+b
3√2·1/4$\pi$+b = √2
b = ¹/₃ -1/4$\pi$
De formule van de raaklijn zou bij mij dan worden:
k(x)=3√2·x+(1/3-1/4$\pi$)
In het antwoordenboek staat:
k(x)=3√2·x+√2-3/4$\pi$√2

Kan iemand uitleggen waar ik precies een fout maak en hoe het dan wel moet??
Alvast bedankt.

Groeten van Iris
Iris v
Leerling bovenbouw havo-vwo - woensdag 24 maart 2004

Antwoord

Beste Iris,

Je wilt dus de vergelijking van de raaklijn in het punt x=¹/₄$\pi$ van de functie f(x)=4·(sin(x))³ op stellen (je mag uiteraard ook f(x)=4·sin³(x) schrijven).

^ Je kunt het m.b.v. standaardformules oplossen ^

Er bestaat een algemene formule voor de linearisering in een punt, die staat op je formulekaart 'lineaire benadering van f in a : L(x)=f(a)+f'(a)·(x-a)', in ons geval is a=¹/₄$\pi$.
Je ziet dat er f'(a) in de formule staat, dus moeten we de afgeleide bepalen.

f(x)=4·sin³(x)
f'(x)=4·(sin³(x))' [de regel g(x)=c·f(x)$\Rightarrow$g'(x)=c·f'(x)]
om (sin³(x))' te bepalen gaan we een beroep doen op de kettingregel. Stel u = sin(x) en y=u³, dan is ^du/_dx=cos(x), en ^dy/_du=3u² = 3·sin²(x). Nu de afgeleide schakels met elkaar vermenigvuldigen, ^dy/_dx=3·cos(x)·sin²(x). Maar er stond nog een 4, dus is f'(x)=4·3·cos(x)·sin²(x) $\Rightarrow$ f'(x)=12·sin²(x)·cos(x). Maar jouw manier klopt ook, hoewel je beter kunt vereenvoudigen.

Er staat in de formule dat we f'(a) = f'(¹/₄$\pi$) moeten gebruiken, dit kunnen we al berekenen, f'(¹/₄$\pi$)=12·sin²(¹/₄$\pi$)·cos(¹/₄$\pi$). Je kunt opzoeken in een tabel dat sin(¹/₄$\pi$) = ¹/₂√2, dus sin²(¹/₄$\pi$) is (¹/₂√2)² = ¹/₂.
En cos(¹/₄$\pi$) is eveneens ¹/₂√2. Dus krijgen we f'(¹/₄$\pi$) = 12·¹/₂·¹/₂√2 = 3√2.

f(a) kunnen we ook al direct invullen (hadden we ook als eerste kunnen doen uiteraard), f(¹/₄$\pi$)=4·sin³(¹/₄$\pi$) $\Rightarrow$ f(¹/₄$\pi$)=4·(¹/₂√2)³ = √2 (ga dit na!).

En dan zijn we klaar, want L(x)=√2 + 3√2·(x-¹/₄$\pi$) en dit kun je herschrijven tot L(x)=3√2·x+√2-³/₄√2·$\pi$.

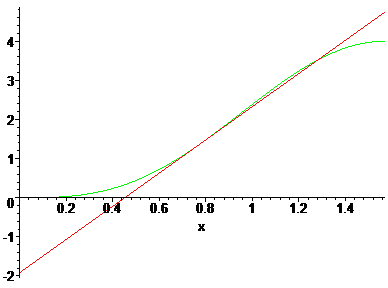
De groene grafiek stelt f(x) voor, en de rode grafiek is de vergelijking van de raaklijn (L(x)). Ter informatie x=¹/₄$\pi$ is ongeveer x=0,79 dus dan weet je waar je moet zoeken.

^ Wat jij fout hebt gedaan ^

De richtingscoëfficiënt heb je correct berekend, die is 3√2, de y-waarde in het punt x=¹/₄$\pi$ is inderdaad √2. De standaard formule voor een eerstegraadsfunctie is f(x)=ax+b waarbij a de richtingscoëfficiënt (3√2), en we weten dat voor x=¹/₄$\pi$ dit gelijk moet zijn aan √2, dus f(¹/₄$\pi$)=3√2·¹/₄$\pi$ + b, en dat moet gelijk zijn aan √2, dus 3√2·¹/₄$\pi$ + b = √2.

Tot zover heb je het goed gedaan, maar nu komt 't. We gaan 3√2·¹/₄$\pi$ herschrijven tot ³/₄√2·$\pi$ dat mag want we hebben alleen de volgorde van de factoren van de vermenigvuldiging veranderd (dit mag, want de vermenigvuldiging in $\mathbf{R}$ is commutatief). Dan krijgen we ³/₄√2·$\pi$ + b = √2.
b = √2 - ³/₄√2·$\pi$

En dan zijn we klaar, want in y=ax+b is je a en b bekend, dus y=3√2·x + √2 - ³/₄√2·$\pi$ en dat hadden we op de standaardmanier ook uitgekregen.

Groetjes,

Davy.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 24 maart 2004