|
|
|
\require{AMSmath}
Vergelijkingen met wortel en veel oplossingen
Ik heb de volgende vergelijking welke meerdere antwoorden oplevert.
1/2b2+bÖ(b2-87/2b)2-431/2
De antwoorden die ik eenvoudig vond zijn 1 en Ö87. Deze vond ik door de formule uit te schrijven en de wortel weg te werken door te kwadrateren met + en - gedeelte van wortel.
Het antwoord 3, of 5 kan ik echter niet vinden door deze methode toe te passen (of ik doe iets fout).
Is er een mogelijkheid om alle antwoorden van deze functie te vinden, zonder ze allemaal te proberen? Een grafiek toonde veel meer oplossingen dan 2, of 3.
c.p.
Iets anders - donderdag 11 maart 2004
Antwoord
Laten we eerst eens goed kijken naar dat gedeelte met die wortel.
Als (b2-87)/(2b) 0 dan is dit gelijk aan (b2-87)/(2b), als
(b2-87)/(2b) 0 dan is dit gelijk aan -((b2-87)/(2b)).
Dus als (b2-87)/(2b)0 dan wordt de hele uitdrukking:
1/2b2+b*(b2-87)/(2b)-43.5=1/2b2+1/2(b2-87)-43.5=b2-87.
Als (b2-87)/(2b)0 dn wordt de hele uitdrukking:
1/2b2-b*(b2-87)/(2b)-43.5=1/2b2-1/2(b2-87)-43.5=0
Als bÖ87 of als -Ö87b0, dan is (b2-87)/(2b)0 en dus de uitdrukking gelijk aan b2-87
Als 0bÖ87 of b-Ö87 dan is (b2-87)/(2b)<0 en dus de uitdrukking gelijk aan 0, wat tot gevolg heeft dat er dus oneindig veel "oplossingen" zijn.
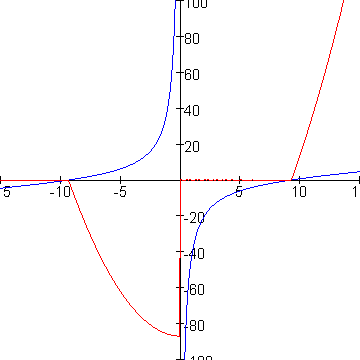
Hieronder zie je dat in de grafiek:
In rood de grafiek van jouw uitdrukking. In blauw de grafiek van (b2-87)/(2b)
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 11 maart 2004
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
