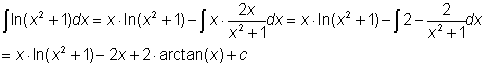WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Integreren

hallo !!
Ik vind de oplossing van òln (x²+1) niet
zou u mij kunnen helpen ?
ik dacht zoiets van:
I= ln·(x³/3)-ò(x³/3)·1/x·dx
I= ln·(x²+1)·x-òx·1/x·((2x³+3x²)/(6))dx
ln·(x²+1)·x-1/6òx·1/x·(2x³+3x²)dx
I=ln·(x²+1)·x-2ò((x²+1)-1)/(x²+1))dx

maar het klopt blijkbaar niet !!

Alvast bedankt
A. Joo
3de graad ASO - woensdag 11 februari 2004

Antwoord

Inderdaad, het klopt heel erg niet!
Je kunt ln niet los zien van (x²+1).
ln is de naam van een functie, die zonder 'iets wat je er in stopt' geen waarde heeft.
Dus ln(x²+1) is een geheel.
Verder gebeuren er nog veel meer gruwelijke dingen in jouw uitwerking, waar we maar niet te lang bij stil moeten staan.
Wat je wel goed gedacht hebt, is: het zal wel met partiële integratie moeten. Dat klopt.
Ik zal hier uitwerken hoe het moet.

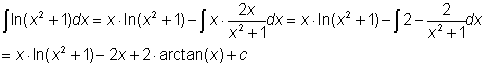
succes verder,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 11 februari 2004