|
|
|
\require{AMSmath}
Re: Veelhoeken en de formule van Pick
Zou je misschien de formule kunnen geven want ik kom er nog steeds niet uit!!
Alvast bedankt
tom he
Leerling bovenbouw havo-vwo - maandag 26 januari 2004
Antwoord
Voor driehoeken waarvan de hoekpunten op roosterpunten liggen bestaat er een interessant verband tussen het aantal roosterpunten (B) op de driehoek, het aantal roosterpunten op de rand van de driehoek (R) en de oppervlakte van de driehoek (O).
B = O + 1/2R + 1
Zie Formule van Pick
Voorbeeld driehoek met gat
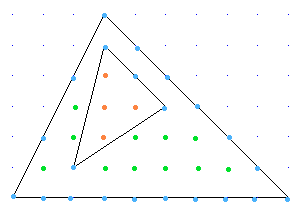
Bij dit soort figuren kan je de formule twee keer toepassen.
Eerst de grote driehoek:
B=37
R=18
Er geldt: 37 = O + 9 + 1, dus O = 27
De kleine driehoek:
B=8
R=4
Er geldt: 8 = O + 2 + 1, dus O = 5
De oppervlakte van de driehoek met gat is 22.
Een directe formule
Voor de grote driehoek geldt:
B = O + 1/2R + 1
O = B - 1/2R - 1
Voor de kleine driehoek geldt:
b = o + 1/2r + 1
o = b - 1/2r - 1
Oppervlakte = O-o = B - 1/2R - 1 - (b - 1/2r - 1)
Opp = B - 1/2R - 1 - b + 1/2r + 1
Opp = B - 1/2R - b + 1/2r
Enzovoort... misschien kan je iets 'leuks' verzinnen, zodat je alle punten maar één keer hoeft te tellen, als je begrijpt wat ik bedoel. Kijk maar naar de kleurtjes in de tekening van het voorbeeld.
Succes!
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 26 januari 2004
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 7588