WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Logaritmische functies

er zijn drie gegeven functies:

F(x)= Ln x
G(x)= 2 Ln x
H(x)= 2+ Ln x

De grafieken snijden van de lijn x=P met 1Pe² (e als van Euler) gelijke stukken af. Bereken P

Ik heb totaal geen idee hoe ik dit kan oplossen, als jullie me kunnen helpen, graag erbij hoe jullie het gedaan hebben het antwoord weer ik al wel.
Harm
Cursist vavo - donderdag 22 januari 2004

Antwoord

Hieronder staan de grafieken van F, G en H in een figuur getekend.

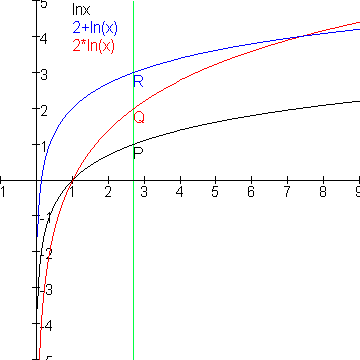
De grafieken van F en G snijden elkaar in (1,0)
De grafieken van G en H snijden elkaar in (e^2,4)
P(p,ln(p)) is het snijpunt van de lijn x=p met de grafiek van F.
Q(p,2ln(p)) is het snijpunt van de lijn x=p met de grafiek van G.
R(p,2+ln(p)) is het snijpunt van de lijn x=p met de grafiek van H.

Kennelijk moet Q midden tussen P en R liggen, dus:
2ln(p)=¹/₂(ln(p)+2+ln(p))
2ln(p)=¹/₂(2ln(p)+2)
2ln(p)=ln(p)+1
ln(p)=1
p=e

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 22 januari 2004