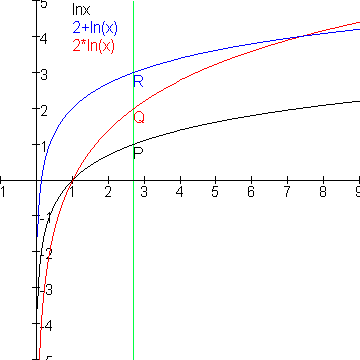
F(x)= Ln x
G(x)= 2 Ln x
H(x)= 2+ Ln x
De grafieken snijden van de lijn x=P met 1
 P
P e2 (e als van Euler) gelijke stukken af. Bereken P
e2 (e als van Euler) gelijke stukken af. Bereken PIk heb totaal geen idee hoe ik dit kan oplossen, als jullie me kunnen helpen, graag erbij hoe jullie het gedaan hebben het antwoord weer ik al wel.
Harm
22-1-2004