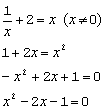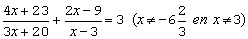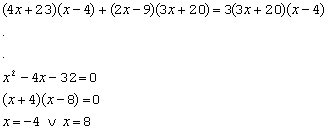|
|
|
\require{AMSmath}



Stelling van Schur
De stelling van Schur zegt:
elke nxn-matrix over C is unitair gelijkvormig met een driehoeksmatrix waarvan de diagonaalcomponenten de eigenwaarden van de matrix zijn.
elke nxn-matrix over R met enkel reŽle eigenwaarden is orthogonaal gelijkvormig met een reŽle driehoeksmatrix waarvan de diagonaalcomponenten de eigenwaarden van de matrix zijn.
nu is mijn vraag: hoe bewijs ik dit?
Dirk
Student universiteit - zaterdag 10 januari 2004
Antwoord
Hallo Don,
Werk eerst de breuk weg, dus alle termen vermenigvuldigen met x
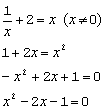
ontbinden lukt niet, dus moet je de a,b,c formule gebruiken.
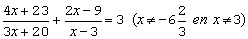
Om de breuken weg te werken moeten we alle termen vermenigvuldigen met (3x+20)(x-4)
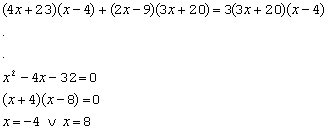
Zie http://www.cs.ut.ee/~toomas_l/linalg/lin1/node17.html

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 14 januari 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|