WisFaq!

Stelling van Schur

De stelling van Schur zegt:
elke nxn-matrix over C is unitair gelijkvormig met een driehoeksmatrix waarvan de diagonaalcomponenten de eigenwaarden van de matrix zijn.
elke nxn-matrix over R met enkel reële eigenwaarden is orthogonaal gelijkvormig met een reële driehoeksmatrix waarvan de diagonaalcomponenten de eigenwaarden van de matrix zijn.

nu is mijn vraag: hoe bewijs ik dit?

Dirk
10-1-2004

Antwoord

Hallo Don,

Werk eerst de breuk weg, dus alle termen vermenigvuldigen met x


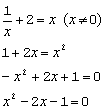
ontbinden lukt niet, dus moet je de a,b,c formule gebruiken.



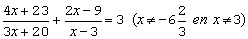
Om de breuken weg te werken moeten we alle termen vermenigvuldigen met (3x+20)(x-4)

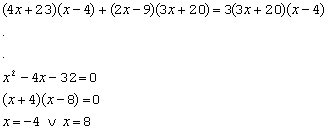
Zie http://www.cs.ut.ee/~toomas_l/linalg/lin1/node17.html [http://www.cs.ut.ee/~toomas_l/linalg/lin1/node17.html]

WvR
14-1-2004