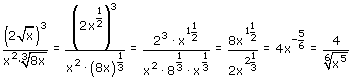WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Asymptoten en andere dingen

Ik heb in de kerstvakantie (fijn) alle sommen van het hoofdstuk (Exponentiele functies) 'opnieuw' gemaakt. Bij het maken van deze sommen, waren er een aantal onduidelijk heden. Ik zit dit jaar in de vierde, en heb dus allemaal vage boeken, nieuwe methodes en dingen worden echt niet helder uitgelegd.

Maar goed, dan nu m'n (vele) vragen:

1) f(x)=2·2^x+1-1

Hoe schrijf ik hier de horizontale asymptoot van op?
Hoe pak ik dat aan?

2) (³/₄)²³⁵·(⁴/₃)²³⁶
Hoe bereken ik dit?

3) Ik zie niet dat (Ö2)³ = 2Ö2 is...

4) (2Öx)³/ x²·³Ö8x = x^-5/6
De vraag is dan ja, schrijf in stappen op hoe dit is gedaan...
Maar dan kom ik niet echt ver want:
(2·x^¹/₂)³ / x²(8x)tot de macht ¹/₃ =
8·x tot de macht 1¹/₂ / x²·8x tot de macht ¹/₃ =
En ehh verder kom ik niet..

BVD
yaggie
Leerling bovenbouw havo-vwo - vrijdag 2 januari 2004

Antwoord

1.
Je hebt een asymptoot als x nadert naar min oneindig.
2·2^x+1 wordt dan 0. Omdat er staat -1 komt de functiewaarde steeds dichter bij -1 te liggen.
De asymptoot: y=-1

2.
Eén van de rekenregels op Rekenregels machten en logaritmen zegt:

M6. (a · b)^p = a^p · b^p

Deze regel kan je ook van rechts naar links gebruiken!
Schrijf (³/₄)²³⁵·(⁴/₃)²³⁶ als:
(³/₄)²³⁵·(⁴/₃)²³⁵·⁴/₃
...zou het dan lukken?

3.
Ö2·Ö2·Ö2=Ö(2·2·2)=Ö8=Ö(4·2)=2Ö2
of
Ö2·Ö2·Ö2=2Ö2

4.
Schrijf alle wortels als machten en gebruik de Rekenregels machten en logaritmen.

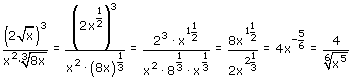
Kijk maar eens goed! Zou het zo lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 2 januari 2004