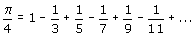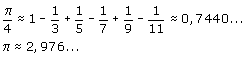|
|
|
\require{AMSmath}



Reeksen van Gregory en Brouncker
Ik snap niet hoe je een kettingbreuk moet uitrekenen? moet je de stappen 1+ 12/3 , 2+ 32/52, enz steeds delen of optellen of iets anders?
En hoe weet je bij de tweede wat je voor x moet invullen en wat komt er dan uit? is het antwoord wat eruit komt dan p? Of iets anders? Dat zijn de dingen die ik niet snap..
Marian
Leerling bovenbouw havo-vwo - dinsdag 30 december 2003
Antwoord
Brouckner
De kettingbreuk is lastig. Eigenlijk staat er dit:

Om U0 te bereken heb je U1 nodig, maar om U1 te berekenen heb je U2 nodig, enz... en dat houdt natuurlijk niet op.
Als je nu 4/p wil benaderen met een n aantal termen, dan neem je Un+1=2n+1.
Voorbeeld
We kiezen n=3.
We willen dus uitrekenen:
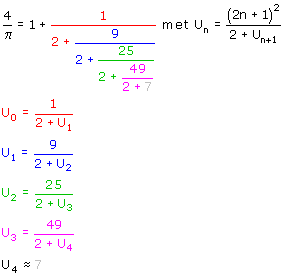
We nemen dan U4=7, we krijgen dan:
4/p 1+1/(2+9/(2+25/(2+49/(2+7))))=1,2717... 1+1/(2+9/(2+25/(2+49/(2+7))))=1,2717...
Dit levert als benadering p 3,1452... 3,1452...
Voor grotere n wordt de benadering dan steeds beter. Probeer het maar eens:
Gregory
Je kunt hier x=1 nemen. Er staat dan arctan(1) en dat is gelijk aan 1/4p. Je krijgt dan:
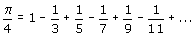
Hoe meer termen je neemt hoe beter de benadering voor 1/4p, waarmee je een benadeing voor p gevonden hebt.
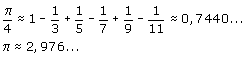
Zoals je ziet schiet het niet erg op. Probeer maar:
Zie bron

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 30 december 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|









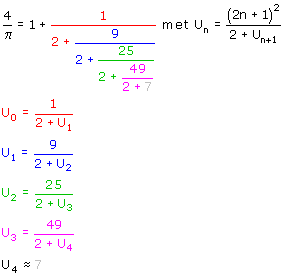
 1+1/(2+9/(2+25/(2+49/(2+7))))=1,2717...
1+1/(2+9/(2+25/(2+49/(2+7))))=1,2717...