WisFaq!

Reeksen van Gregory en Brouncker

Ik snap niet hoe je een kettingbreuk moet uitrekenen? moet je de stappen 1+ 1²/3 , 2+ 3²/5², enz steeds delen of optellen of iets anders?

En hoe weet je bij de tweede wat je voor x moet invullen en wat komt er dan uit? is het antwoord wat eruit komt dan p? Of iets anders? Dat zijn de dingen die ik niet snap..

Marian
30-12-2003

Antwoord

Brouckner
De kettingbreuk is lastig. Eigenlijk staat er dit:



Om U₀ te bereken heb je U₁ nodig, maar om U₁ te berekenen heb je U₂ nodig, enz... en dat houdt natuurlijk niet op.

Als je nu 4/p wil benaderen met een n aantal termen, dan neem je U_n+1=2n+1.

Voorbeeld
We kiezen n=3.
We willen dus uitrekenen:



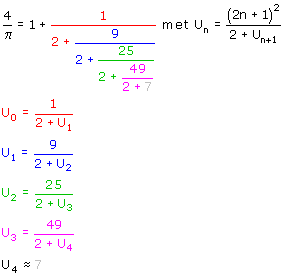
We nemen dan U₄=7, we krijgen dan:

⁴/_p1+1/(2+9/(2+25/(2+49/(2+7))))=1,2717...
Dit levert als benadering p3,1452...

Voor grotere n wordt de benadering dan steeds beter. Probeer het maar eens:

Gregory
Je kunt hier x=1 nemen. Er staat dan arctan(1) en dat is gelijk aan ¹/₄p. Je krijgt dan:



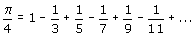
Hoe meer termen je neemt hoe beter de benadering voor ¹/₄p, waarmee je een benadeing voor p gevonden hebt.



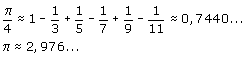
Zoals je ziet schiet het niet erg op. Probeer maar:

Zie bron [http://www.sciences-en-ligne.com/momo/chronomath/anx3/pi_brouncker.html]

WvR
30-12-2003