|
|
|
\require{AMSmath}



Driehoek van Pascal en het binomium van Newton
hallo,
Ik had een vraagje over de driehoek van Pascal. Wanneer je de rijen van bovenaf nummert, beginnent bij 0 en je kijkt naar de rijen waarvan het nummer een priemgtal is, dan zie je dat alle termen in deze rij deelbaar zijn door het rijnummer (behalve de enen natuurlijk). Hoe kan ik dit bewijzen?
Alvast bedankt
groetje Greetje
Greetj
Student hbo - woensdag 10 december 2003
Antwoord
Beste Greetje,
Het ke element (tellend te beginnen met 0) van rij p (p priem) kan worden berekend met
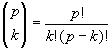
Omdat de enen niet meedoen, weten we dat k 0. Duidelijk is dat k! en (p-k)! de p niet uit de teller weg kunnen delen, omdat k en p-k kleiner zijn dan p. Het resultaat zal dus nog steeds deelbaar zijn door p. 0. Duidelijk is dat k! en (p-k)! de p niet uit de teller weg kunnen delen, omdat k en p-k kleiner zijn dan p. Het resultaat zal dus nog steeds deelbaar zijn door p.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 december 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








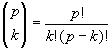
 0. Duidelijk is dat k! en (p-k)! de p niet uit de teller weg kunnen delen, omdat k en p-k kleiner zijn dan p. Het resultaat zal dus nog steeds deelbaar zijn door p.
0. Duidelijk is dat k! en (p-k)! de p niet uit de teller weg kunnen delen, omdat k en p-k kleiner zijn dan p. Het resultaat zal dus nog steeds deelbaar zijn door p.

