WisFaq!

Driehoek van Pascal en het binomium van Newton

hallo,

Ik had een vraagje over de driehoek van Pascal. Wanneer je de rijen van bovenaf nummert, beginnent bij 0 en je kijkt naar de rijen waarvan het nummer een priemgtal is, dan zie je dat alle termen in deze rij deelbaar zijn door het rijnummer (behalve de enen natuurlijk). Hoe kan ik dit bewijzen?

Alvast bedankt

groetje Greetje

Greetje van Broekhoven
10-12-2003

Antwoord

Beste Greetje,

Het k^e element (tellend te beginnen met 0) van rij p (p priem) kan worden berekend met



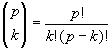
Omdat de enen niet meedoen, weten we dat k0. Duidelijk is dat k! en (p-k)! de p niet uit de teller weg kunnen delen, omdat k en p-k kleiner zijn dan p. Het resultaat zal dus nog steeds deelbaar zijn door p.

FvL
10-12-2003