WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Een punt op een cirkel berekenen adhv een rotatie

Dit is een reactie op vraag 17122

Gegeven:
# Middelpunt: (5;5)
# Punt a: (8;8)
# Rotatie: 20°

Ingevuld:
bx = 8.0,94 - 8.0,34 = 4,8 + 5 = 9,8
by = 8.0,94 + 8.0,34 = 10,24 + 5 = 15,24

Punt b zou dus (9,8 ; 15,24) zijn. Als de rotatie tegen de klok in loopt, zou het punt b volgens
een tekening nochtans rond het punt (9 ; 6,5) moeten liggen.

Wat heb ik (weeral) verkeerd gedaan?
E Geys
Student Hoger Onderwijs België - dinsdag 9 december 2003

Antwoord

Misschien was mijn uitleg niet volledig.
De coördinaat a(x_a,y_a) is de coördinaat t.o.v. je assenstelsel met het middelpunt van de cirkel als oorsprong.

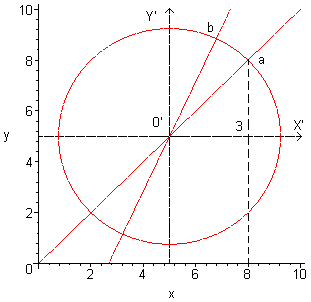
Eerst verschuiven we het assenstelsel tot de oorsprong samenvalt met het middelpunt van de cirkel.
De coördinaat van a tov dat nieuwe (X',Y')-assenstelsel is dan a(3,3).

Toepassing van de formules geeft ons voor de b(x'_b,y'_b) in het (X',Y')-assenstelsel:
x'_b=3cos(20°)-3sin(20°)=1.79
y'_b=3cos(20°)+3sin(20°)=3.845

Dus: b(x_b,y_b) = (6.79, 8.845) in het oorspronkelijke assenstelsel.

Mvg,

Els

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 december 2003