WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Deel een driehoek in vijf driehoeken met gelijke oppervlakte

De opdracht is om een allereerst een gelijkbenige driehoek ABC te verdelen in vijf gelijke delen. Hoek A is een rechte hoek. Vanuit die hoek begin je een zigzaglijn naar lijnstuk BC, vanuit daar weer terug naar AB. Je hebt nu al 2 driehoeken. Vanuit AB trek je de lijn door naar BC en vervolgens weer terug naar AB. Zo zou je vijf driehoeken moeten creeren, met gelijke oppervlakte.

Maar hoe moet ik dit doen als ik een willekeurige rechthoekige driehoek heb?

En kan dit ook met een willekeurige driehoek?
Lotte
Student hbo - zondag 7 december 2003

Antwoord

Laten we dan maar beginnen met een willekeurige driehoek. De situatie die je wilt is:

De driehoeken hebben allemaal dezelfde oppervlakte. Dat betekent dat:
4·O($\Delta$CAP)=O($\Delta$ABP)
(De oppervlakte van de gele driehoek is 4 keer de oppervlakte van de blauwe driehoeken samen)

Dat betekent dat 4·CP=BP
O($\Delta$CAP)=1/2·CP·h
O($\Delta$ABP)=1/2·BP·h
Kortom zet P zo dat 4·PC=BP. Daarmee kan je dus je eerste punt P vinden. Concreet: neem aan dat BC=5 dan is CP=1 en BP=4.

De andere punten Q, R en S kan je op dezelfde manier vinden, alleen dan met de verhouding 3:1, 2:1 en 1:1. Waarmee S kennelijk op het midden van QB ligt.

Construeren
Kan je nu een willekeurig lijnstuk in 5 gelijke delen verdelen door middel van een constructie?
Ja dat kan! Kijk maar eens hieronder:

Applet werkt niet meer.
Download het bestand.

Hopelijk kan je er nu verder mee...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 7 december 2003

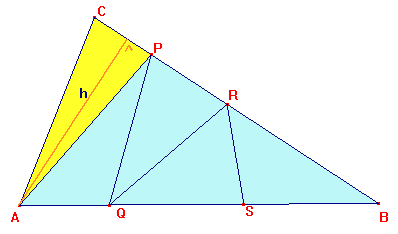
Re: Deel een driehoek in vijf driehoeken met gelijke oppervlakte