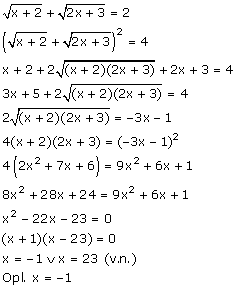|
|
|
\require{AMSmath}



Oefeningen tweedegraads vergelijkingen
(x2+x)2-14(x2+x)+24=0y-1 16
--- = ---
y+1 y2-1 Ö(x+2)+Ö(2x+3)=2
oscar
2de graad ASO - vrijdag 28 november 2003
Antwoord
1.
Neem y=x2+x, dan:
y2-14y+24=0
(y-2)(y-12)=0 (zie Vergelijkingen oplossen m.b.v. ontbinden in factoren)
y=2 of y=12
Dus nu oplossen:
x2+x=2
x2+x-2=0
(x+2)(x-1)=0
x=-2 of x=1
x2+x=12
x2+x-12=0
(x+4)(x-3)=0
x=-4 of x=3
Dus: s={-4, -2, 1, 3}
2.
Kruislings vermenigvuldigen:
(y-1)(y2-1)=16·(y+1)
Hier ligt het voor de hand de haakjes te gaan werkwerken. Maar dat moet je niet doen, je kunt meteen proberen te ontbinden in factoren:
(y-1)(y-1)(y+1)-16(y+1)=0 (Zie verschil van twee machten)
(y+1){(y-1)2-16)=0
y+1=0 of (y-1)2-16=0
y=-1 of (y-1)2=16
y=-1 of y-1=4 of y-1=-4
y=-1 of y=3 of y=-3
s={-3, -1, 3}
3.
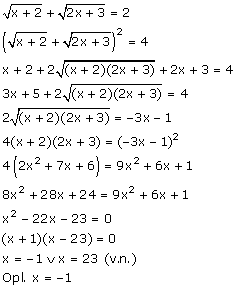
Oplossen als altijd en wel controleren of de gevonden oplossingen inderdaad voldoen. Door het kwadrateren kan je 'verkeerde' oplossingen krijgen.
Zou het zo lukken?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 1 december 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|