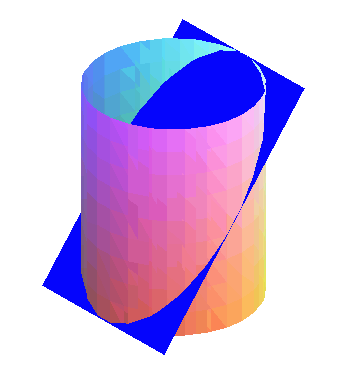WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Gecombineerde straal

Dit is een reactie op vraag 16466

Aan het Wis-Faq team,

Na een lange discussie dien ik, denk ik, de vraag wat meer toe te lichten;

De vraag gaat over een gestuurde boorkop die moet afwijken van zijn rechte lijn. Zo'n afwijking gebeurt via een bepaalde straal. De gewenste straal wordt m.i. gedefinieerd door twee cilinders welke op hun beurt weer gedefinieerd worden door de geprojecteerde stralen in het horizontale en het verticale vlak. De richting (hoek t.o.v. rechte lijn) van de afwijking is variabel.

Als de hoek van de afwijking en de beide stralen in het horizontale en verticale vlak bekend zijn, wat is dan de formule van de gecombineerde straal?

Alvast bedankt voor de moeite
Maarte
Iets anders - maandag 24 november 2003

Antwoord

dag Maarten,

Ik blijf er bij dat de straal in het verticale vlak (dus de cilinder die horizontaal loopt) niet vrij gekozen kan worden als je al gekozen hebt voor de straal in het horizontale vlak en de hoek van het boorvlak met het horizontale vlak.
De eenvoudigste aanpak is dan: zie de bijgaande figuur.

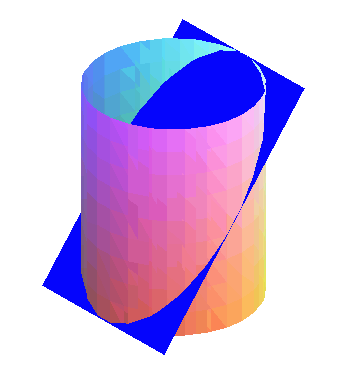
Het blauwe vlak is het vlak waarin de kromme ligt die de boorkop volgt.
Het gaat dus om de straal van de doorsnede van het blauwe vlak met de cilinder, en wel in het punt van het bovenvlak.
De tweedimensionale figuur die de doorsnede weergeeft, moet dus in dat punt benaderd worden met een cirkel.
De straal in het horizontale vlak noem ik r.
De hoek van het blauwe vlak met het horizontale vlak is bekend, zeg $\alpha$, dus daarmee kun je de hoogte van de cilinder berekenen.
Ik noem de halve hoogte h.
(dus tan($\alpha$) = h/r)
De straal van de benaderende cirkel is dan gelijk aan:
r²/√(r² + h²)
(dit heet ook wel: kromtestraal).
Ik hoop dat dit een bevredigend antwoord op je vraag is.
Met vriendelijke groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 24 november 2003