WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gecombineerde straal

Indien een cirkelboog wordt gedefiniëerd door één cirkelboog met een bekende straal in een vlak en een andere cirkelboog met een bekende straal in een ander vlak hoe bereken je dan de straal van de resulterende cirkelboog?
De beide bekende cirkelbogen starten in hetzelfde punt en de hoek tussen de twee vlakken is alfa.
Maarte
Iets anders - vrijdag 21 november 2003

Antwoord

Uit je toelichting blijkt dat de hoek $\alpha$ een rechte hoek is, dus de vlakken staan loodrecht op elkaar.
In dat geval is het verband tussen de stralen simpel:
r is de straal in het horizontale vlak
R is de straal in het verticale vlak,

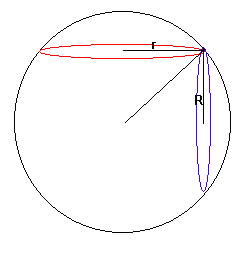
dan is de gecombineerde straal gelijk aan √(r²+R²)
(met behulp van de stelling van Pythagoras).
Als de hoek tussen de vlakken gelijk is aan $\alpha$, dan wordt het iets ingewikkelder:

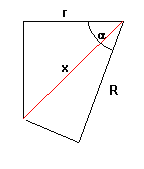
x is de gezochte gecombineerde straal.
$\alpha$ = $\alpha$₁+$\alpha$₂, dus:
cos($\alpha$) = cos($\alpha$₁+$\alpha$₂) = cos($\alpha$₁)·cos($\alpha$₂) - sin($\alpha$₁)·sin($\alpha$₂)
De cosinus en sinus van deze deelhoeken zijn uit te drukken in x, r en R, en
cos($\alpha$) zelf is bekend, dus dat levert een vergelijking in x, r en R, die oplosbaar is (een kwadratische vergelijking in x²).
Lukt dat verder?
succes.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 21 november 2003

Re: Gecombineerde straal