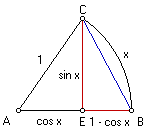WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lim (cos x - 1)/x berekenen met eenheidscirkel

Dit is een reactie op vraag 16478

Is ook bekend hoe je zonder al te veel voorkennis de limiet naar nul kunt berekenen van ^cos(x)-1/_x? Ik denk hierbij bijvoorbeeld aan eveneens een gebruik van de eenheidscirkel...

Een stap van de 'insluiting' is makkelijk.
cos(x)$<$1 voor x uit (0,1) $\Rightarrow$ ^cos(x)-1/_x$<$0 voor x voldoende klein. Rest te vinden een functie f(x) zodanig dat f(x)$<$^cos(x)-1/_x met f(x) naar 0 als h naar 0?

Tine
Iets anders - zondag 23 november 2003

Antwoord

Beste Tine,

Jouw probleem is inderdaad tamelijk eenvoudig op te lossen. We gebruiken de volgende figuur.

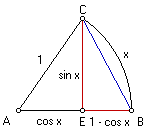
In deze figuur is de boog BC (van lengte x) natuurlijk groter dan het lijnstuk BC, zodat we met Pythagoras in driehok BCE kunnen afleiden:

x² $>$ sin² x + (1-cos x)²

oftewel

(1-cos x)² $<$ x² - sin² x.

Dit kunnen we natuurlijk uitbreiden naar

0 $<$ (1-cos x)² $<$ x² - sin² x

en na deling door x² wordt dit

0 $<$ (^{(1-cos x)}/_x)² $<$ 1 - (^{sin x}/_x)².

Met de vraag waar je op reageert weten we dat (^{sin x}/_x$\to$1 voor x$\to$0, zodat het rechterlid van de laatste ongelijkheid die we kregen naar 0 gaat voor x$\to$0, en dus moet het ingesloten lid ook naar 0 gaan. En dan gaat zijn wortel natuurlijk ook naar 0, en ook het tegengestelde van die wortel, dus ^(cos(x)-1)/_x .

Naschrift:
Tine kwam met de volgende reactie, die ik de lezer niet wil onthouden:

Deze oplossing is ook mooi :-)... bedankt.
Ik had ondertussen het volgende gevonden:
(1-cos x)(1+cos x) = 1-cos²x = sin² x $<$ x²
zodat ^{(1-cos x)}/_x $<$ ^x/_{(1+cos x)} waaruit het gestelde volgt...

gonio rules...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 23 november 2003