WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lim sin(x)/x berekenen met eenheidscirkel

Hoi,

Mijn vraag is hoe je de limiet van sinx/x kan berekenen m.b.v de eenheidscirkel. Van de eenheidscirkel begrijp ik weinig van, daarom heb ik er moeite mee.
In mijn boek staat:

sin x $<$ x $<$ tan x
1 $<$ x/xsin $<$ 1/cosx
1 $>$ sinx/x $>$ cos x.

Ik begrijp niet hoe ze hieraan gekomen zijn met de eenheidscirkel.

Alvast bedankt!
Peter
Peter
Leerling bovenbouw havo-vwo - vrijdag 21 november 2003

Antwoord

Beste Peter,

Je moet in elk geval weten hoe je de sinus en de tangens met de eenheidscirkel kan vinden. Zie daarvoor vraag 6217 voor een directe uitleg van de sinus en een link naar een uitleg voor de tangens. Ik neem verder aan dat je bekend bent met het gebruik van radialen.

De situatie laat zich schetsen met het volgende plaatje

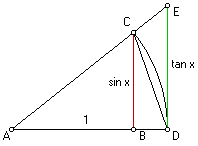
Bij de boog DC moet je x denken, zoals dat bij de definitie van radialen gebruikelijk is.

Van belang is nu dat je ziet dat de oppervlakte van het cirkelsegment ADC gelijk is aan ¹/₂ x. Dat kun je inzien doordat de oppervlakte van de hele cirkel $\pi$ is en de hele omtrek 2$\pi$. Als je je nu voorstelt dat je het punt C laat draaien, dan loopt de omtrek DC dus twee keer zo hard als de oppervlakte van het segment ADC. Immers, uiteindelijk is de volle omtrek het dubbele van de volle oppervlakte.

De oppervlakte van $\Delta$ADC is ¹/₂·AD·BC = ¹/₂sin x, en de oppervlakte van $\Delta$ADE is ¹/₂·AD·DE = ¹/₂tan x.

Duidelijk is in de figuur dat de oppervlakte van $\Delta$ADC kleiner is dan het cirkelsegment, en de oppervlakte van $\Delta$ADE groter.

We concluderen dat sin x $<$ x $<$ tan x.

Delen door sin x levert: 1 $<$ ^x/_{sin x} $<$ ¹/_{cos x}.

Alles vervangen door zijn omgekeerde (dus .. vervangen door ¹/_.., let op dat nu de tekens om moeten klappen) geeft: 1 $>$ ^{sin x}/_x $>$ cos x.

Nu weten we dat als x$\to$0, dan cos x$\to$1.
En met bovenstaande dus ook ^{sin x}/_x$\to$1.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 21 november 2003

Lim (cos x - 1)/x berekenen met eenheidscirkel

Re: Lim sin(x)/x berekenen met eenheidscirkel