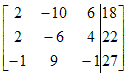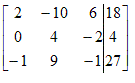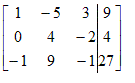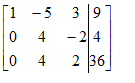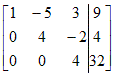WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Stelsel vergelijkingen oplossen met matrix-notatie

Dit is een reactie op vraag 13397

Ik begrijp niet hoe u aan die 0.5 (2de rij, 2de kolom) komt, en aan 10? Van 6 naar 10? Die stap begrijp ik niet. Kunt u door stap voor stap het vegen uit te leggen, misschien duidelijker mbv een 3x3 matrix, mij duidelijk maken hoe precies het vegen werkt. Uit de andere opgaven is mij dit niet duidelijk geworden
Liza v
Student universiteit - woensdag 12 november 2003

Antwoord

Hoi Liza,
Hieronder een voorbeeld hoe je matrices kunt gebruiken om een stelsel van vergelijkingen op te lossen. Zoals je voorstelt heb ik een 3×3 matrix als voorbeeld genomen.

Nemen we het volgende stelsel vergelijkingen:

2A - 10B + 6C = 18
2A - 6B + 4C = 22
-A + 9B - C = 27

Dan kunnen we dit ook op een andere manier noteren met matrices. Dat zou er dan als volgt uitzien:

$
\left[ {\begin{array}{*{20}c}
2 & { - 10} & 6 \\
2 & { - 6} & 4 \\
{ - 1} & 9 & { - 1} \\
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}c}
A \\
B \\
C \\
\end{array}} \right] = \left[ {\begin{array}{*{20}c}
{18} \\
{22} \\
{27} \\
\end{array}} \right]
$

Nog korter zouden we dat kunnen schrijven als:

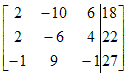
Hier zie je meteen het voordeel van deze manier van noteren. Dit is een stuk korter dan elke keer het hele stelsel uit te schrijven en je hebt minder kans op fouten.

Om het schoonvegen van matrices makkelijker te kunnen begrijpen is het goed om je te realiseren dat het hetzelfde is als dat stelsel waar je mee begon.

Het vegen van de matrix geeft je een heel gestructureerde manier van aanpak. Het doel is in de onderdriehoek van de matrix allemaal nullen te krijgen. Dan vind je eenvoudig de waarde van C en daarmee uit de regel daarboven B en dan A.

Kijken we naar ons stelsel vergelijkingen dan zou je waarschijnlijk beginnen de eerste vergelijking van de tweede af te trekken.
Je krijgt dan het volgende stelsel:

2A - 10B + 6C = 18
2A - 6B + 4C -2A +10B -6C= 22 -18
-A + 9B - C = 27

dus:

2A - 10B + 6C = 18
4B - 2C = 4
-A + 9B - C = 27

Let op het aftrekken van een negatief getal!!
In de notatie van onze matrix is dat hetzelfde als de hele eerste rij van de tweede af te trekken:

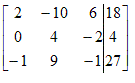
De eerste rij blijft dan gewoon onveranderd staan!

Wat je ook altijd bij een vergelijking mag doen is de hele vergelijking met een bepaald getal vermenigvuldigen of door een bepaald getal delen. (Let wel op bij 0!)
Zo mag je de eerste vergelijking in ons stelsel delen door 2.
2A - 10B + 6C = 18 wordt dan:
A – 5B + 3C = 9

Dat mag je dus ook in de matrix:

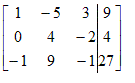
Zo gaan we verder. Nu tellen we de eerste regel bij de laatste op:

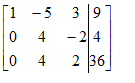
Dan trekken we de tweede rij van de derde af:

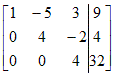
Dus
A-5B+3C =9
4B - 2C = 4
4C = 32
en daarom
A = 10
B = 5
C = 8

Je kunt ook verder gaan in de matrix notatie. Dat zou dan als volgt eruit zien:

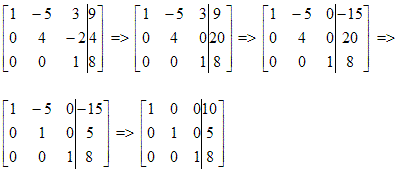
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 13 november 2003