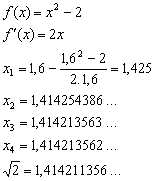|
|
|
\require{AMSmath}



Newton Raphson methode
De Newton-Raphson methode is een methode waarbij je door middel van iteraties de nulpunten kan benaderen.
De formule die je hiervoor gebruikt is:
I1 = I0 - ( f(I0) / F'(I0) )
Maar hoe moet je deze formule invullen als je bijvoorbeeld de nulpunten van de formule 2x3 + 2x2 + x + 4 wil weten. Hoe moet ik dan gebruik maken van bovenstaande formule?
Hoe kan ik met deze methode de nulpunten van de functie
f:x - 5x3 -6x -2 berekenen? ( er zijn 3 verschillende nulpunten) 5x3 -6x -2 berekenen? ( er zijn 3 verschillende nulpunten)
Welke methoden zijn er nog meer om de 0 punten te berekenen? zijn dit
Bisectie
Secant
Newton
Muller
Halley
Annika
Leerling bovenbouw havo-vwo - woensdag 12 november 2003
Antwoord
Hallo Annika,
voorbeeld:
De nulpunten van f(x) = x2 – 2 zijn x = -√2 en x = √2.
Als we deze nulpunten willen benaderen met de methode van Newton-Raphson
Dan vinden we uitgaande van x0 = 1,6
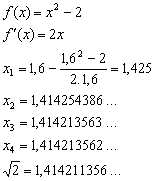
Om een benadering van -√2 te vinden moet je een andere startwaarde kiezen b.v. x0 = -2
Als je weet dat een functie drie nulpunten heeft dan moet je wel weten wat die ongeveer zijn.
Met de GRM is dit geen probleem.
y1 = gegeven functie
y2 = afgeleide van de gegeven functie
Kijk eerst waar de de functie de x-as ongeveer snijdt.
stel we kiezen voor x0 = -2
Dan voeren we in het basisscherm in:
-2 gevolgd door [ENTER]
-2
ANS-y1(ANS)/y2(ANS)
Als we nu een aantal keer op [ENTER] drukken dan vinden we een benadering van het nulpunt dat het dichts bij –2 ligt.
wl
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 november 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 5x3 -6x -2 berekenen? ( er zijn 3 verschillende nulpunten)
5x3 -6x -2 berekenen? ( er zijn 3 verschillende nulpunten)