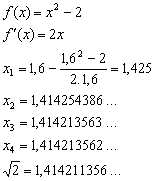WisFaq!

Newton Raphson methode

De Newton-Raphson methode is een methode waarbij je door middel van iteraties de nulpunten kan benaderen.
De formule die je hiervoor gebruikt is:
I1 = I0 - ( f(I0) / F'(I0) )

Maar hoe moet je deze formule invullen als je bijvoorbeeld de nulpunten van de formule 2x³ + 2x² + x + 4 wil weten. Hoe moet ik dan gebruik maken van bovenstaande formule?

Hoe kan ik met deze methode de nulpunten van de functie
f:x - 5x³ -6x -2 berekenen? ( er zijn 3 verschillende nulpunten)

Welke methoden zijn er nog meer om de 0 punten te berekenen? zijn dit
Bisectie
Secant
Newton
Muller
Halley

Annika van Bussel
12-11-2003

Antwoord

Hallo Annika,

voorbeeld:

De nulpunten van f(x) = x² – 2 zijn x = -√2 en x = √2.

Als we deze nulpunten willen benaderen met de methode van Newton-Raphson
Dan vinden we uitgaande van x₀ = 1,6



Om een benadering van -√2 te vinden moet je een andere startwaarde kiezen b.v. x₀ = -2

Als je weet dat een functie drie nulpunten heeft dan moet je wel weten wat die ongeveer zijn.

Met de GRM is dit geen probleem.

y₁ = gegeven functie
y₂ = afgeleide van de gegeven functie

Kijk eerst waar de de functie de x-as ongeveer snijdt.
stel we kiezen voor x₀ = -2

Dan voeren we in het basisscherm in:

-2 gevolgd door [ENTER]
-2
ANS-y₁(ANS)/y₂(ANS)

Als we nu een aantal keer op [ENTER] drukken dan vinden we een benadering van het nulpunt dat het dichts bij –2 ligt.

wl
12-11-2003