De digitale vraagbaak voor het wiskundeonderwijs

home |  vandaag |  gisteren |  bijzonder |  gastenboek |  wie is wie? |  verhalen |  contact

HOME

samengevat

vragen bekijken

een vraag stellen

hulpjes

zoeken

FAQ

links

twitter

boeken

help

inloggen

colofon

Straal omgeschreven cirkel

Gegeven: een gelijkbenige driehoek met als basis 4 cm en opstaande zijden 6 cm.

Ik weet dan hoe ik de omgeschreven cirkel moet construeren, maar ik weet niet hoe ik de straal van deze cirkel moet berekenen.

h
2de graad ASO - zaterdag 11 oktober 2003

Antwoord

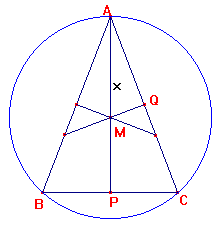Noem de top A en de andere hoekpunten B en C. Noem P het midden van BC en Q het midden van AC. De bewuste middelloodlijnen snijden elkaar in M, het middelpunt van de omgeschreven cirkel.

|AP| kan je berekenen. Stel |AM|=x, dan is |MP|=|AP|-x.
Er geldt ook dat |MC|² = |MP|² + |PC|², en dat moet ook gelijk zijn aan |AM|², aangezien zowel |MC| als |AM| de straal voorstellen. Oplossen naar x en klaar is kees. Als het niet lukt vraag je maar extra uitleg.

Vragen naar aanleiding van dit antwoord? Klik rechts..! zaterdag 11 oktober 2003

Re: Straal omgeschreven cirkel

home |  vandaag |  bijzonder |  gastenboek |  statistieken |  wie is wie? |  verhalen |  colofon

©2001-2025 WisFaq - versie 3