WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoek tussen kruisende rechten

Piramide TABCD met ABCD grondvlak en T top. ABCD is rechthoek en snijpunt vd diagonaolen van deze rechthoek is M. TDC=90°=ADT. Op ribbe TC ligt punt P in het midden van deze ribbe met TD=4, DC=AB=4, AD=BC=3
Gevraagd: bewijs dat MPB=HOEK(TA,PB) en bereken die hoek als je weet dat TD loodrecht staat op DB
Dotje
3de graad ASO - dinsdag 9 september 2003

Antwoord

Eerst maar eens een tekening:

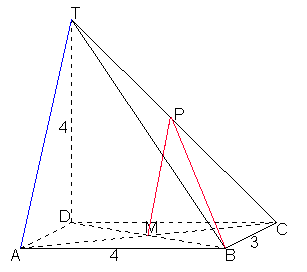
Kijk eens naar DACT. M ligt op het midden van AC en P ligt op het midden van CT. MP is dan de middenparallel van DACT, dus AT//MP. De hoek tussen de (kruisende) rechten AT en BP is dan (vanwege de evenwijdigheid) hetzelfde als ÐBPM. Zou het zo lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 9 september 2003

Re: Hoek tussen kruisende rechten