|
|
|
\require{AMSmath}



Pythagoreďsche drietallen
Wat zijn de zijden van een pythagoreische driehoek als de straal van de ingeschreven cirkel 7 is?
De uitkomsten moeten gehele getallen zijn die onverenigbaar zijn. Er moeten twee oplossingen mogelijk zijn. Een ervan is 15, 112, 113
Jerney
Leerling bovenbouw havo-vwo - maandag 4 februari 2002
Antwoord
 De tweede is 16, 63, 65. De tweede is 16, 63, 65.
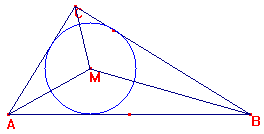
Aanpak: in een rechthoekige driehoek ABC met rechthoekszijden a en b en schuine zijde c teken je de ingeschreven cirkel met middelpunt M en straal 7. Teken de lijnstukken AM, BM en CM.
Nu geldt:
Opp( ABC) = Opp( ABC) = Opp( AMB) + Opp( AMB) + Opp( BMC) + Opp( BMC) + Opp( CMA) CMA)
˝ab = ˝·7(a + b + c)
ab = 7(a + b + c). (*)
Verder geldt voor pythagoreische drietallen a, b en c dat je ze kunt schrijven als:
a = m2 - n2 ; b = 2mn en c = m2-n2
Dit invullen in (*) geeft:
(m2-n2)·2mn = 7(m2-n2+2mn+m2+n2)
(m-n)(m+n)·2mn = 14m(m+n)
(m-n)·n = 7
m = 7/n + n
Maar omdat m en n gehele getallen zijn, kan dit alleen als n = 1 of n = 7.
n=1 geeft m=8, dan heb je a=63, b=16, c=65;
n=7 geeft m=8, dan heb je a=15, b=112, c=113.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 6 februari 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 De tweede is 16, 63, 65.
De tweede is 16, 63, 65.  ABC) = Opp(
ABC) = Opp(
