|
|
|
\require{AMSmath}



Polynoom ontbinden in factoren dmv staartdeling
Hallo,
Zou u mij kunnen vertellen hoe ik een polynoom als
x4-1 zou moeten ontbinden in factoren met behulp van
een staartdeling?
Alvast bedankt!
Joost.
Joost
Student universiteit - donderdag 4 september 2003
Antwoord
Hoi,
Eerst moet je een kandidaat-deler zoeken. Je kan dit makkelijkst door volgende stelling te gebruiken:
Als f(x) een veelterm is en f(a)=0, dan is (x-a) een deler van f(x).
In jouw voorbeeld zien we met f(x)=x4-1 dat f(-1)=f(1)=0. We hebben dus onmiddellijk 2 kandidaat delers: x+1 en x-1.
In volgend plaatje deel ik f(x) door x-1:
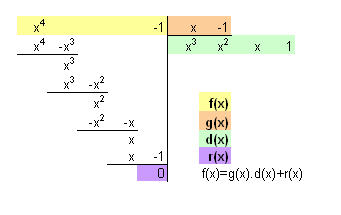
Je ziet dat r(x)=0, zodat d(x) inderdaad een deler is van f(x). Je moet dan d(x) nog delen door x+1. Uiteindelijk vind je: x4-1=(x-1)(x+1)(x2+1)... (Maar dit kon je eigenlijk zo zien  ) )
Groetjes,
Johan
andros
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 4 september 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








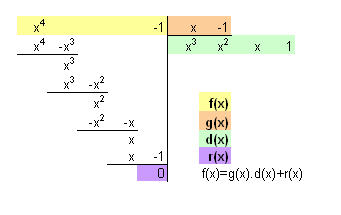
 )
) 