|
|
|
\require{AMSmath}



Oppervlakte formule voor een driehoek
Bewijs dat in een driehoek de volgende oppervlakteformules gelden
S=1/4·(b²+c²-a²)tana
Deze oefening is eigelijk bedoeld voor mijn vakantietaak, maar ik heb er echt al uren op zitten staren zonder enig resultaat, ik weet echt niet hoe ik er aan moet beginnen, cosinusregel, stelling van pythagoras?
kunt u mij aub helpen
alvast bedankt
amber
2de graad ASO - zaterdag 30 augustus 2003
Antwoord
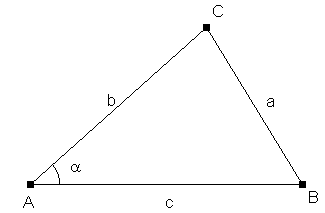
Twee formules:
oppervlakteformule: s = 1/2·b·c·sin(a)
cosinusregel: a2 = b2 + c2 - 2·b·c·cos(a)
Als je deze twee formules combineert krijg je de gegeven formule! De vraag is nog even hoe..., maar kijk maar eens goed.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 30 augustus 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










