WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bewijs alpha is een scherpe hoek

sina=Ö(1-cos²a)
cosa=Ö(1-sin²a)
nele
Overige TSO-BSO - dinsdag 19 augustus 2003

Antwoord

Hoi,

Je gebruikt sin²a + cos²a = 1

Dus sin²a = 1 - cos²a
sina = ±Ö(1 - cos²a)

cos²a = 1 - sin²a
cosa = ±Ö(1 - sin²a)

sina = ±Ö(1 - cos²a)

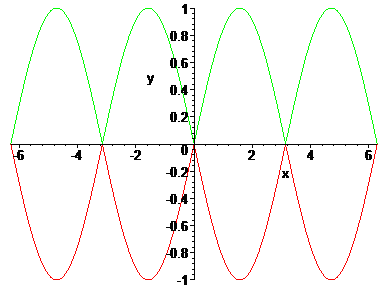
De groene grafiek is Ö(1 - cos²a) en de rode grafiek is -Ö(1 - cos²a). Wanneer vallen deze grafieken samen met de echte sinusfunctie?
Als de groene grafiek wordt afgebeeld op het interval [0,p], [2p,3p], ... maar ook van [-2p, p], [-4p, -3p] etc. Dus algemeen a Î [0 + 2kp, p + 2kp] waarbij k Î .
De rode grafiek valt samen met de sinusfunctie voor [p,2p] maar ook van [3p,4p], ... maar ook van [-p,0], [-3p,0] enz. Algemeen [a Î p + 2kp, 2p + 2kp] waarbij k Î .
Maar dat is de volledige sinusfunctie, we moesten alleen rekeninghouden met de sinus van de scherpe hoek, dus als a ligt tussen 0 + 2kp, ¹/₂p + 2kp of 1¹/₂p + 2kp, 2p + 2kp. Dit laatste is de scherpe negatieve hoek (als je dus met de klok mee draait).
Dus de grafiek van Ö(1 - cos²a) geef de sinus van de scherpe hoek van a weer op het interval 0 + 2kp, ¹/₂p + 2kp en de grafiek van -Ö(1 - cos²a) geef de sinus van de negatieve scherpe hoek van a op het interval 1¹/₂p + 2kp, 2p + 2kp.

De andere functie gaat analoog, probeer die dan ook zelf. Indien je er niet uitkomt, kom dan nog eens terug.

Groetjes,

Davy.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 19 augustus 2003