|
|
|
\require{AMSmath}



Re -gonio functie
Hallo wisfaq,
Ik had eerder een vraag gesteld maar ik was het domein vergeten te geven, waardoor mijn vraag niet beantwoord kon worden. Ik zal het nogmaals opschrijven.
geg: fp(x)= 2cos(x)(sin2x-p) Domein : x E [0,2p]
gevr: Bepaal de waarden van p waarvoor fp precies 6 nulpunten heeft.
Kunt u dit a.u.b in kleine stapjes laten zien, want hier begrijp ik niets van.
Timmy
Leerling bovenbouw havo-vwo - maandag 18 augustus 2003
Antwoord
Hallo Timmy,
fp(x)=0 als
cos(x)=0 of (sin2(x)-p)=0
cos(x)=0 heeft op het domein [0,2p] 2 oplossingen n.l. x=0,5p en x=1,5p.
We moeten dus p zo kiezen dat (sin2(x)-p)=0 precies 4 oplossingen heeft.
sin2(x)=p®sin(x)=-Öp of sin(x)=Öp.
Als 0 p p 1 dan heeft sin(x)=Öp op het domein [0,2p] 2 oplossingen. (1 in het eerste kwadrant en 1 in het tweede kwadrant) 1 dan heeft sin(x)=Öp op het domein [0,2p] 2 oplossingen. (1 in het eerste kwadrant en 1 in het tweede kwadrant)
Ook sin(x)=-Öp heeft 2 oplossingen.(1 in het derde kwadrant en een in het vierde kwadrant)
Conclusie: voor 0 p p 1 heeft fp precies 6 nulpunten. 1 heeft fp precies 6 nulpunten.
Dat sin2(x)=p voor 0 p p 1 precies 4 oplossingen heeft volgt ook uit de onderstaande grafiek. 1 precies 4 oplossingen heeft volgt ook uit de onderstaande grafiek.
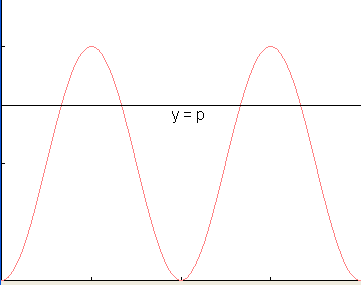
wl
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 18 augustus 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|








 p
p
