WisFaq!

Re -gonio functie

Hallo wisfaq,

Ik had eerder een vraag gesteld maar ik was het domein vergeten te geven, waardoor mijn vraag niet beantwoord kon worden. Ik zal het nogmaals opschrijven.

geg: fp(x)= 2cos(x)(sin²x-p) Domein : x E [0,2p]

gevr: Bepaal de waarden van p waarvoor fp precies 6 nulpunten heeft.

Kunt u dit a.u.b in kleine stapjes laten zien, want hier begrijp ik niets van.

Timmy
18-8-2003

Antwoord

Hallo Timmy,

f_p(x)=0 als
cos(x)=0 of (sin²(x)-p)=0
cos(x)=0 heeft op het domein [0,2p] 2 oplossingen n.l. x=0,5p en x=1,5p.
We moeten dus p zo kiezen dat (sin²(x)-p)=0 precies 4 oplossingen heeft.
sin²(x)=p®sin(x)=-Öp of sin(x)=Öp.
Als 0p1 dan heeft sin(x)=Öp op het domein [0,2p] 2 oplossingen. (1 in het eerste kwadrant en 1 in het tweede kwadrant)
Ook sin(x)=-Öp heeft 2 oplossingen.(1 in het derde kwadrant en een in het vierde kwadrant)

Conclusie: voor 0p1 heeft f_p precies 6 nulpunten.

Dat sin²(x)=p voor 0p1 precies 4 oplossingen heeft volgt ook uit de onderstaande grafiek.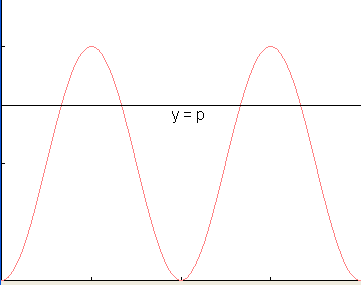

wl
18-8-2003