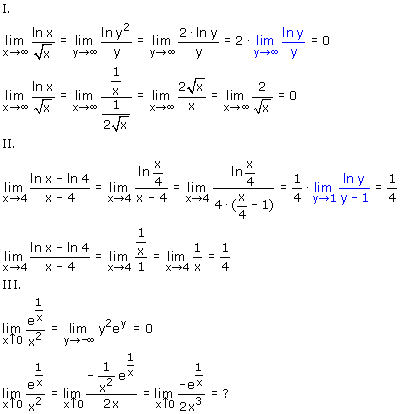|
|
|
\require{AMSmath}



Re: Re: Limieten berekenen lukt niet
Ja, ik weet het, maar ik heb heel lang in de database gezocht naar de regel van de l'Hôpital en begrijp de principe alleen weet ik niet wat ik verkeerd doe,dat wil ik graag weten, bovendien krijg ik in 6 vwo wel de regel van l'hopital dus wilde ik het nu beide manieren begrijpen, maar als jullie me dat niet willen laten zien, dan begrijp ik dat.
Groetjes
Zafarp
Leerling bovenbouw havo-vwo - maandag 14 juli 2003
Antwoord
Regel van de l'Hôpital
Laat f en g:(a,b)\to\mathbf{R}.
Als:- f en g differentieerbaar zijn op (a,b)
- g'(x) \ne 0 op (a,b)
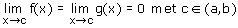
dan is 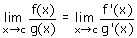
bron: Vraagstukken Analyse - Al & Edelaar
Voorbeeld:
Gevraagd 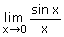
Controleer dat aan de voorwaarden voldaan is!
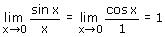
Voorbeeld:
Gevraagd 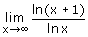
Controleer of aan de voorwaarden voldaan is!
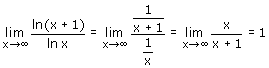
Als het goed is heb je geconstateerd dat dit laatste voorbeeld niet aan de voorwaarden voldoet! Er moest immers gelden dat:
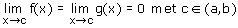
Toch klopt het wel!
Daarom kunnen we beter Almering gebruiken:
Stelling (de l'Hôpital)
Laat de functies f en g differentieerbaar zijn op (a,b),
waarbij a\in\mathbf{R} of a=-\infty, b\in of b=+\infty. of b=+\infty.
Indien geldt:
A) g'(x)\ne0 voor alle x\in(a,b) en
B) 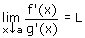 , waarbij L\in , waarbij L\in of L=-\infty of L=+\infty, of L=-\infty of L=+\infty,
terwijl voldaan is aan één van de volgende voorwaarden:
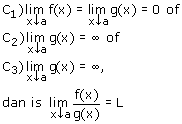
Een analoge uitspraak geldt voor x b en x\toc waarbij in het laatste geval (a,b) vervangen moet worden door een gereduceerde r-omgeving van c\in\mathbf{R}. b en x\toc waarbij in het laatste geval (a,b) vervangen moet worden door een gereduceerde r-omgeving van c\in\mathbf{R}.
Met behulp van deze voorwaarden kan er niet veel meer misgaan. Hieronder zie je nog een paar voorbeelden (eerst met standaardlimieten, daarna met de l'Hopital). Het laatste voorbeeld is interessant, omdat daar blijkt dat als je de l'Hopital kan toepassen dat niet wil zeggen dat je daar altijd iets mee opschiet.
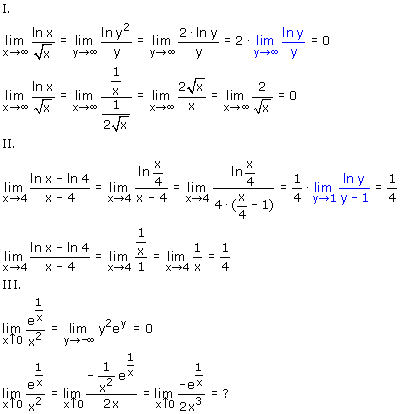

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 14 juli 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|








 Dit is een reactie op vraag 13118
Dit is een reactie op vraag 13118 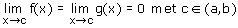
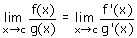
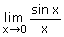
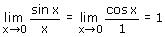
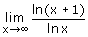
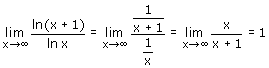
 of b=+
of b=+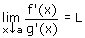 , waarbij L
, waarbij L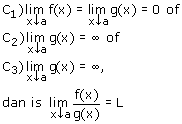
 b en x
b en x