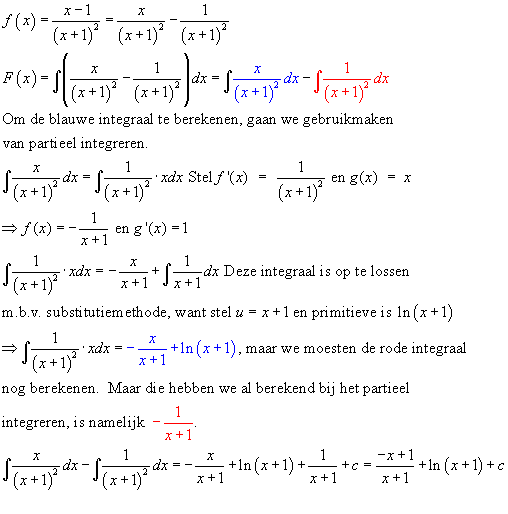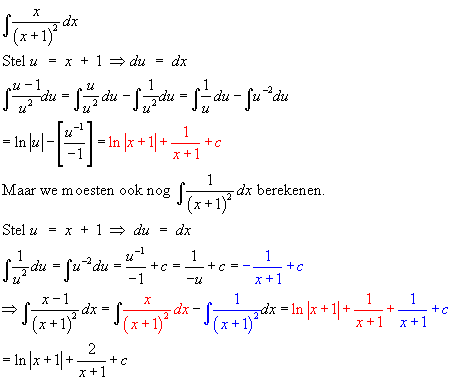|
|
|
\require{AMSmath}



Re: Primitieven bepalen
Hallo Davy,
Dank u voor het beantwoorden van mijn vraag, alleen snap ik niet precies hoe u van ...maakt (zie onder)
1/2x2+ 1/(x-2) = x2(x-2)+2/(2(x-2)) ik denk dat u 1/2x2 vermenigvuldigt met de noemer(x-2) klopt dat ?
Dan had ik nog een vraag; "ze" vragen met de functie die u heeft geprimitiveerd om de oppervlakte te berekenen van het vlakdeel ingesloten door de x-as de y-as en de grafiek van f.
Maar de primietive die ze noteren op mijn antwoorden blad is anders dan u primietive namelijk:
f(x)= x-1/(x+1)2
F(x)= lnx + 1 + (2)/(x+1) maar hoe komen ze dan daaraan ? En wat wordt de oppervlakte dan ?
Ik hoop dat u voor meer duidelijkheid kan scheppen.
Nogmaals bedankt voor u antwoord alvast.
Shadi
Leerling bovenbouw havo-vwo - vrijdag 4 juli 2003
Antwoord
Hoi,
Ik neem aan dat jij het over het groene gedeelte hebt, dat heb ik gekregen door x2/2 én 1/(x - 2) op gelijke noemer te zetten, namelijk 2(x - 2), daarvoor heb ik x2 vermenigvuldigd met (x - 2) en 1 vermenigvuldigd met 2, krijg je [x2·(x - 2) + 2]/[2(x - 2)] en dat kan nog herschrijven worden tot (x3 - 2x2 + 2)/(2x - 4).
Dan het tweede gedeelte. Ik heb die opgave anders geïnterpreteerd omdat je geen haakjes hebt gebruikt. Je bedoelde als functie f(x) = (x - 1)/(x + 1)2 dus x - 1 volledig in de teller en (x+1)2 volledig in de noemer, en dat is niet het enige want nu geef je een andere functie, eerst gaf je l(x)= (x-1)/(x-2)2 op, maar nu f(x) = (x-1)/(x+1)2, maar goed...
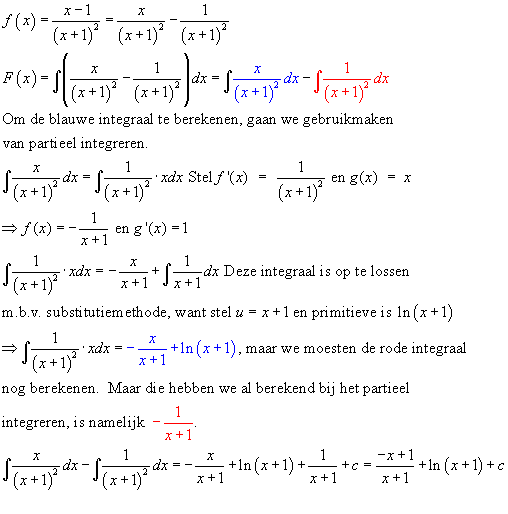
Het antwoordenboekje gaf dus als antwoord F(x) = ln(x+1) + 2/(x+1), maar als je mijn antwoord differentieert kom je op precies dezelfde beginfunctie f(x) = (x-1)/(x+1)2 uit. Als je gaat rekenen met mijn uitkomst en de uitkomst die gegeven werd door het antwoordenboekje dan kom je telkens een verschil van 1 uit, dus er moet iets misgegaan zijn, want als substitutie lukt dan is partieel integreren niet de aangewezen methode en dit heeft tot een fout antwoord geleid.
Misschien kunnen we 't gemakkelijker aanpakken? De fout moet duidelijk in de integraal van x/(x+1)2 zitten. Laten we die integraal 'ns anders oplossen.
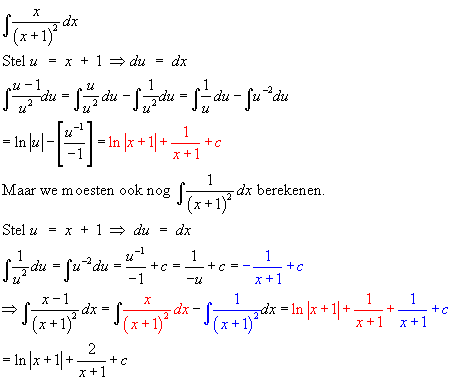
Groetjes,
Davy.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 5 juli 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 12996
Dit is een reactie op vraag 12996