WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Primitieven bepalen

Hoi wisfaq,

Ik ben voor het eerst bezig met een hoofstuk over integreren en het vinden van primitieven van functies, alleen begrijp de regels niet zo goed.

als men de volgende functie heeft:

f(x)= 1/x² dan is de primietive: F(x)=-1/x

Maar als ik deze functie heb:

g(x)=12/x² krijgt men de dan G(x) door de quotientregel te gebruiken of moet men de standaard primietive "ombouwen" tot:

G(x)= -12/x ?? als men de quotientregel moet gebruiken zou u dat dan aub willen laten zien.

Ook weet ik niet wanneer ik bij functies zoals daarboven de standaard primitieve moet gebruiken, of gebruik moet maken van de quotientregel. b.v bij de volgende functie;

l(x)= x-1/(x-2)² hoe bepaalt men de primitieve hiervan ??

Wilt u aub korte stapjes gebruiken,ik vind integreren zeer lastig.

Alvast hartelijk bedankt.
Shadi
Leerling bovenbouw havo-vwo - vrijdag 4 juli 2003

Antwoord

Beste Shadi,

Eerst probeer ik je uit te leggen waarom de primitieve van 1/x² gelijk is aan -1/x.
Je kunt f(x) = 1/x² herschrijven als x^-2.
F(x) kan bepaald worden door de regel òxⁿdx = ^{x^{n + 1}}/_{(n + 1)}.
Hier toegepast F(x) = ^{x^{-2 + 1}}/_{(-2 + 1)} = ^{x^-1}/_-1 = -1/x.

Dan g(x) = 12/x², dat is hetzelfde als 12 · 1/x², en een constante mag voor het integraalteken gezet worden, krijgen we 12ò1/x²dx = 12òx^-2dx = 12·x^-1/_(-1) + c = ¹²/_-x + c = ^-12/_x.

Ter controle moeten we deze functie gaan differentiëren en dat kunnen we m.b.v. de quotiëntregel doen, algemeen gaat die regel (f/g)' = (gf' - fg')/g². ^{[x·(-12)' - (-12)·x']}/_x² = ^{0 + 12}/_x² = ¹²/_x² en da's de oorspronkelijke functie dus de primitieve klopt.

Dan de volgende

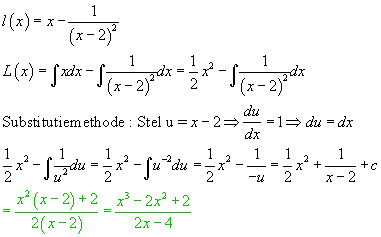
Je zou de primitieve wederom moeten differentiëren om na te gaan of de primitieve correct is, maar neem maar van mij aan dat ie klopt. Dat groene zou je trouwens kunnen weglaten.

Indien er iets onduidelijk is, reageer gerust op dit antwoord.

Groetjes,

Davy.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 4 juli 2003

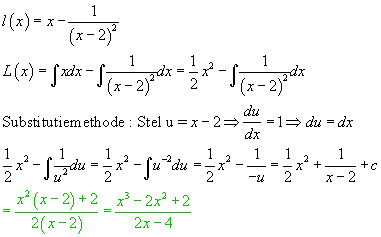
Re: Primitieven bepalen