 |
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
||||||||||||||||||
|
\require{AMSmath}



Re: Re: Minimum
Ja, veel kans dat het boek fout is. Maar wat ik wel opmerk is dat jij |pb| als onbekende invoert.Volgens mij moet je |a'p| als onbekende y stellen bijvoorbeeld , en in functie daarvan |pb'| berekenen, zodanig dat als je de som maakt je enkel in functie rekent van het gevraagde. De functie gelijk aan nul stellen wordt zeer veel gedaan, maar het zou ook kunnen zijn dat je deze voor een minimum niet nul moet stellen. Het zou ook kunnen zijn bijvoorbeeld dat de som een minimum vormt als |a'p| en |pb'| de rechthoekszijden van een rechthoekige driehoek vormen. De schuine zijde wordt dan |a'b'| en die zou je kunnen berekenen met de volgende manier: Links heb je 20 en rechts 60, dus aan de linkerkant heb je dan een rechthoekszijde van 40 en de horizontale rechthoekszijde is dan die 90 zodanig dat de verbindingslijn van a' en b' de schuine zijde van deze rechthoekige driehoek vormt = ÷(402 + 902) = 10÷97 . We hebben dan de vergelijking : |a'p|2 + |pb'|2 = 9700, dit uitwerken leidt eveneens tot oplossingen, maar niet 102,96, het zou dus om een andere constante kunnen gaan ... In alle geval, een goed gevonden truukje heh ? AntwoordHallo Berten,



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2025 WisFaq - versie 3
| ||||||||||||||||||

 Dit is een reactie op vraag 12827
Dit is een reactie op vraag 12827 
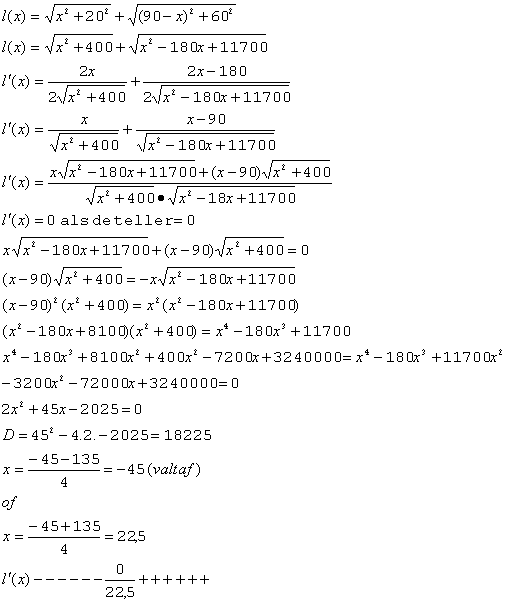
 120,42.
120,42.