Re: Re: Minimum

Dit is een reactie op vraag 12827

Ja, veel kans dat het boek fout is. Maar wat ik wel opmerk is dat jij |pb| als onbekende invoert.Volgens mij moet je |a'p| als onbekende y stellen bijvoorbeeld , en in functie daarvan |pb'| berekenen, zodanig dat als je de som maakt je enkel in functie rekent van het gevraagde. De functie gelijk aan nul stellen wordt zeer veel gedaan, maar het zou ook kunnen zijn dat je deze voor een minimum niet nul moet stellen. Het zou ook kunnen zijn bijvoorbeeld dat de som een minimum vormt als |a'p| en |pb'| de rechthoekszijden van een rechthoekige driehoek vormen. De schuine zijde wordt dan |a'b'| en die zou je kunnen berekenen met de volgende manier: Links heb je 20 en rechts 60, dus aan de linkerkant heb je dan een rechthoekszijde van 40 en de horizontale rechthoekszijde is dan die 90 zodanig dat de verbindingslijn van a' en b' de schuine zijde van deze rechthoekige driehoek vormt = Ö(40² + 90²) = 10Ö97 . We hebben dan de vergelijking : |a'p|² + |pb'|² = 9700, dit uitwerken leidt eveneens tot oplossingen, maar niet 102,96, het zou dus om een andere constante kunnen gaan ... In alle geval, een goed gevonden truukje heh ?

berten
3de graad ASO - vrijdag 27 juni 2003

Antwoord

Hallo Berten,

Je gaat er dan wel vanuit dat de hoek a'pb' gelijk is aan 90 graden.
Verder moet je niet je functie gelijk aan nul stellen maar de afgeleide je functie!!



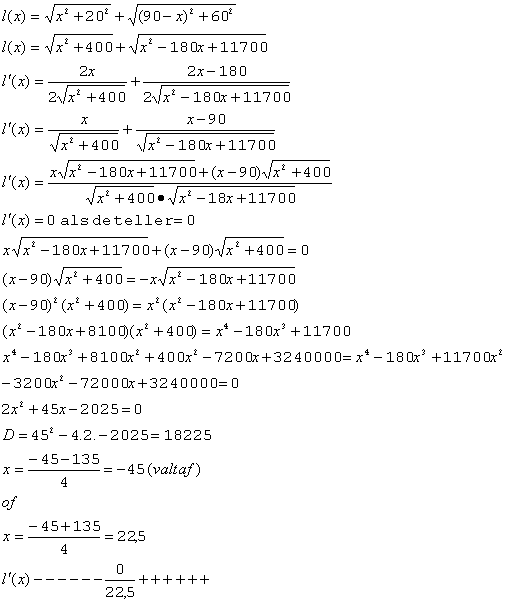
Er is dus een minimum voor x= 22,5.
Dit minimum is gelijk aan l(22,5)120,42.

De onderstaande oplossing is niet van mezelf maar van een collega beantwoorder:

Dit is één van favoriete vraagstukjes...
(als afsluiter voor een se of zo...)
Want als je b' aan de andere kant legt... dan krijg je:
20:x=60:(90-x)
60x=20(90-x)
60x=1800-20x
80x=1800
x=22,5

Flauw he?
Zie Afstand d.m.v. differentiëren

wl
vrijdag 27 juni 2003

©2001-2024 WisFaq