|
|
|
\require{AMSmath}



Toepassen van ab=ac
hoi,
ik probeer AB=AC toe te passen om deze vergelijking op te lossen.
(x-2)2(x-1)= 4(x-2)2
Als antwoordt krijg x=2 of x=5 ,maar voor x= 2 klopt het niet ik denk dat ik een deel van de vergelijking fout doe kunt u misschien laten zien hoe men dit oplost zodat ik het kan zien ?
En deze snap ik ook niet (logx)2= 2logx omdat ze logx in het kwadraat zetten.
Verandert hierdoor ook die regel van AB=AC ?
Bijvoorbaat dank
David
Leerling bovenbouw havo-vwo - woensdag 21 mei 2003
Antwoord
Hoi,
Eerste gedeelte
(x - 2)2·(x - 1) = 4(x-2)2
(x - 2)2·(x - 1) - 4(x - 2)2 = 0
(x - 2)2·[(x-1)-4] = 0
Een product is 0 dan en slechts dan als een van de factoren 0 is
(x - 2)2 = 0 of x - 5 = 0
x = 2 (2 keer vanwege kwadraat) of x = 5
Maar als je twijfelt, plot dan gewoon de twee functies en bepaal dan de snijpunten (pas je x-interval aan je gevonden snijpunten aan).
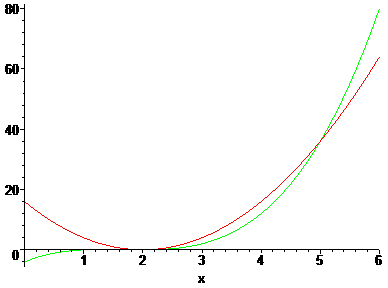
De rode functie is (x-2)2·(x-1) en de groene is 4(x - 2)2 en de snijpunten zijn correct berekend.
Tweede gedeelte
Stel een hulpvariabele a = log(x),
dan geldt a2 - 2a = 0
a(a - 2) = 0
a = 0 of a = 2
maar a = log(x) dus log(x) = 0 of log(x) = 2
x = 1 of x = 102
x = 1 of x = 100
Die hulpvariabele heb ik voor de overzichtelijkheid er neer gezet, je had ook
[log(x)]·(log(x) - 2] = 0 enz. kunnen opschrijven, maar de vorige notatie leek me duidelijker.
Duidelijk?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 21 mei 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










