WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Specifieke uitslag van een kegel

Dit is een reactie op vraag 10712

Beste Anneke,
Als lezer met een verouderd MULO diploma met handel zul je begrijpen dat ik alle zeilen bij moet zetten om je uitleg te snappen. Daarom als het niet te veel moeite is graag een tekeningetje met een eenvoudige doch meervoudig toe te passen gebruiksformule als het maar allemaal niet te veel gevraagd is hoor ????? Je moet n.l het kegeltje of de chatton zoals het in het vakjargon heet aan kunnen passen aan iedere steengrootte . m.v.gr Frans
Frans
Docent - vrijdag 9 mei 2003

Antwoord

Niet te bescheiden hoor. Ga er maar van uit, dat we je graag van dienst zijn.
Hier komt-ie.
De straal r van het grondvlak, de hoogte p van de afgeknotte kegel, en de tophoek t zijn bekend. In jouw geval dus: r=6.5, p=5.5 en t=17°.

Er geldt: tan(t/2)=r/h, dus h=r/tan(t/2)
Dan geldt: h²+r²=a², dus a is bekend.
Vervolgens:
h:p=a:b, dus b=a·p/h
s is de straal van het bovenvlak.
Dan is (a-b):a=s:r, dus s=(a-b)·r/a
Omtrek van het grondvlak is 2pr.
Omtrek van het bovenvlak is 2ps.
Nu de uitslag:

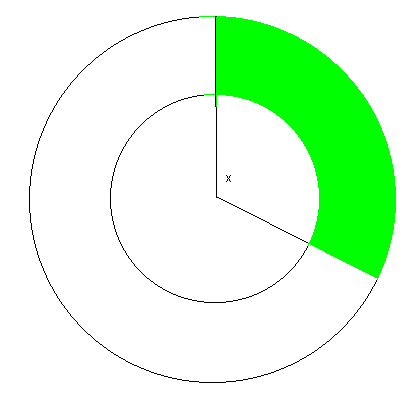
De uitslag is begrensd door twee cirkelbogen, met stralen a en a-b.
De hoek x vanuit de top is bijvoorbeeld te berekenen met de formule: x=2pr/a
Ik hoop dat dit algemeen toepasbaar genoeg is.
succes.
groet, Anneke

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 9 mei 2003