WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oplossen van ongelijkheden

Ik zit met een examensom:
f(x)=√(-2x+12) en g(x)=x-1
De vraag zelf is: los op f(x)$\leq$g(x) en eventuele afrondingen naar 2 decimalen.
I.J. G
Leerling bovenbouw havo-vwo - woensdag 7 mei 2003

Antwoord

Voor het oplossen van ongelijkheden hanteer ik zelf het volgende 'stappenplan'.
Bereken de snijpunten waar het precies gelijk is
Kijk naar domein en eventuele asymptoten
Plot de grafieken
Bepaal de oplossing
Laten we dit maar eens als voorbeeld nemen.

Snijpunten
√(-2x+12)=x-1
-2x+12=(x-1)²
-2x+12=x²-2x+1
x²=11
x=$\,\pm\,$√11
(dit kan eventueel ook met je GR)

Let op: -√11 kan geen oplossing zijn, want de 'uitkomst' van een wortel kan niet negatief zijn. x-1 zou -√11-1 zijn. Bij kwadrateren moet je altijd even controleren of je oplossingen wel voldoen.

Domein en asymptoten
Getallen onder het wortelteken mogen niet kleiner dan 0 zijn. Dus:
-2x+12$\geq$0
-2x$\geq$-12
2x$\leq$12
x$\leq$6

Grafieken plotten

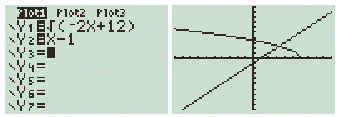
Oplossingen
Waar is nu f(x)$\leq$g(x)?
Ik zie een snijpunt (dat zal dan wel die √11 zijn!) en ik weet dat f(x) niet verder loopt dan x=6. Dus het antwoord moet zijn:
[√11,6]
Of als je de snijpunten benaderd hebt:
[3,22;6]

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 7 mei 2003