WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

123456789

Ik heb dus de volgende opgave gekregen. Je moet de getallen 123456789 zo rangschikken dat:
De 2 laatste getallen moeten deelbaar zijn door 9
Dan moet je het laatste getal laten vallen en moet je de laatste 2 getallen delen door 8
Dan moet je het laatste getal laten vallen en moet je de laatste 2 getallen delen door 7
enzovoort tot 1

Jonas
3de graad ASO - donderdag 1 mei 2003

Antwoord

Ik neem aan dat het volgende plaatje aangeeft wat je vraag is. Twee aan twee zijn cijfers getallen die deelbaar zijn door de getallen 1 tot en met 9.

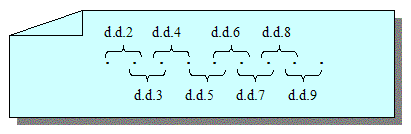
Eerst bekijken we maar eens de kenmerken van deelbaarheid. Dan gaan we stap voor stap de aanwijzingen gebruiken om het antwoord te vinden.

Kenmerken van deelbaarheid:
In het algemeen kun je aan de hand van de volgende kenmerken vrij snel zien of een getal deelbaar is.
alle gehele getallen zijn deelbaar door 1
alle getallen die even zijn; oftewel eindigen op 0, 2, 4, 6 of 8
de som van de cijfers is deelbaar door 3 (b.v. 54321 is dd 3 want 5+4+3+2+1 = 15)
de laatste twee cijfers deelbaar door 4 zijn. Getal moet in ieder geval even zijn.
getal eindigt op 0 of 5
deelbaar door 2 en 3
(dit heeft niet een heel makkelijk deel kenmerk)
de laatste 3 cijfers zijn deelbaar door 8
de som van de cijfers is deelbaar door 9
Deelbaar door 2, 4, 6 en 8
Getallen die deelbaar zijn door 2, 4, 6 en 8 zijn allemaal even. Dat betekent dus dat ze op 2, 4, 6, 8 of 0 eindigen. In deze puzzel hebben we niet de beschikking over 0. De cijfers 2, 4, 6 en 8 worden verdeeld over de vier plekken die deelbaar zijn door 2, 4, 6 en 8; dus we weten nu precies waar de even en waar de oneven getallen moeten komen te staan.

Deelbaar door 5
Zoals we al zagen is een getal deelbaar door 5 als het eindigt met een 0 of 5. We hebben de 0 hier niet tot onze beschikking. Alleen de 5 is dus mogelijk. We hebben de locatie van ons eerste cijfer bepaald.

Deelbaar door 6, 7, 8 en 9
Nu we de plek van de 5 weten kunnen we zo door redeneren voor de deelbaarheid door 6, 7, 8 en 9 en vinden we de volgende 4 cijfers.

Deelbaar door 4
Dan wordt het al iets moeilijker. Kijk eerst eens naar de deelbaarheid door 4. We weten dat het getal dat we moeten delen door 4 begint met een 1 of 7 (alleen deze oneven cijfers zijn over).
Dan zien we al vrij snel dat het alleen kan eindigen met 2 of 6. Maar 6 hebben we al gebruikt. Dus we weten nu de locatie van de 2. De 8 blijft nu over van de even cijfers en ook deze kunnen we nu plaatsen.

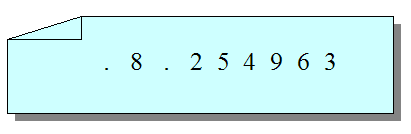
De oplossing
We houden nu 1 en 7 over. Beide overgebleven mogelijkheden zijn mogelijk: we hebben dus twee oplossingen.

Nieuwe puzzel
Nu ik je puzzel heb opgelost heb ik een nieuwe voor jou:
We hebben nu de cijfers 0 1 2 3 4 5 6 7 8 9
Hiermee vormen we een getal van 10 cijfers. Voor dit getal geldt dat het getal gevormd door de eerste i cijfers deelbaar is door i (waarbij i = 1,2,3,.....,10)
Voorbeeld: voor de cijfers 1 2 3 de oplossing zou kunnen zijn: 321
3 is deelbaar door 1
32 is deelbaar door 2
321 is deelbaar door 3

Deze puzzel is wel iets moeilijker dan die hier is opgelost. Maar je kunt wel elementen gebruiken. Veel succes!!!!!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 2 mei 2003

Re: 123456789