Vraag 1:
--------
Pas de stelling van Pythagoras toe in de opstaande driehoeken, die dus allemaal rechthoekig zijn in D. We noemen hierbij de lengte van een rechthoekszijde 'a'
(1) a2=|DA|2+|DC|2
(2) a2=|DB|2+|DC|2
(3) a2=|DA|2+|DB|2
Uit (1) en (2) volgt dat |DA|=|DB|, uit (1) en (3) volgt dat |DB|=|DC|, dus uiteindelijk is |DA|=|DB|=|DC|=aÖ2/2.
Vraag 2:
--------
Met loodrechte spiegeling bedoel je waarschijnlijk loodrechte projectie.
Aangezien |DA|=|DB|=|DC| is ook |GA|=|GB|=|GC| aangezien de driehoeken AGD, BGD en CGD congruent zijn. Het punt G is dus het midden van de driehoek ABC. In de vlakke meetkunde toont men met behulp van Pythagoras of de cosinusregel aan dat |GA|=|GB|=|GC|=aÖ3/3. Probeer dat zelf eens.
Pythagoras in driehoek AGD geeft dan |GD|2+1/3a2=1/2a2 dus |GD|=aÖ6/6. Het volume van het viervlak is nu
V = 1/3|GD| Opp(ABC) = 1/2a3Ö24
Het volume kan je trouwens veel eenvoudiger vinden door het viervlak op een andere vlak te laten rusten en dat als grondvlak te gebruiken. Er komt dan
V = 1/3 (aÖ2/2) 1/2(aÖ2/2)(aÖ2/2) = 1/2a3Ö24
Vraag 3:
--------
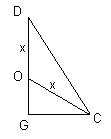
Opnieuw Pythagoras:
|GO|2+ 1/3a2 = x2
|GO|=aÖ6/6-x
Þx=aÖ6/4. Merk op dat dit punt zich dan wel buiten het viervlak bevindt.
Dit is een reactie op vraag 10129 
