|
|
|
\require{AMSmath}


Driehoek met omschreven cirkel
Gevraagd:
Beschouw een gelijkzijdige driehoek ABC met zijde 1. Laat M het middelpunt zijn van de cirkel omschreven rond deze driehoek. Laat punt D het beeld zijn van punt B na muntspiegeling rond M. Wat is de afstand van A tot D?
Wat ik heb geprobeerd:
Door de situatie te schetsen kreeg ik de indruk dat de driehoek ABD te verkrijgen is door punt C te schuiven langs de cirkel tot de positie van punt D, tevens is de afstand BD gelijk aan de diameter van de cirkel. Verder dan dit kom ik helaas niet...
Erik-Jan
Leerling bovenbouw havo-vwo - zondag 26 mei 2024
Antwoord
Hallo Erik-Jan,
Prima om een schets te maken:
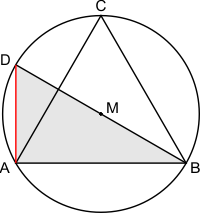
Bekijk driehoek ABD met hoeken 90°, 30° en 60°. De zijden verhouden zich als 1:2:√3. Je weet: AB=1, dus met deze verhoudingen is zijde AD te berekenen.
Lukt het hiermee?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 26 mei 2024
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










 Re: Driehoek met omschreven cirkel
Re: Driehoek met omschreven cirkel