Geneeskunde toelatingsexamen

Beste is er iemand die me zou kunnen helpen met de volgende vraag: wiskunde juli 2017 vraag 1

Dit is de vraag :
In de volgende figuur worden 4 krommen weergegeven.



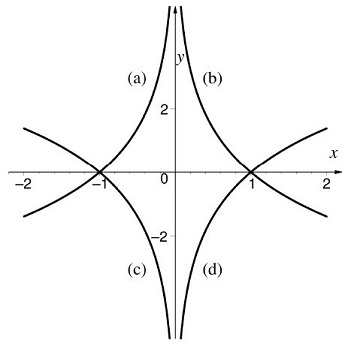
De grafiek van de functie f met functievoorschrift f(x) = -ln(¹/_x²) bestaat uit de unie van welke 2 krommen?

Hoe begin ik hier het best aan om zo snel mogelijk tot een oplossing te komen? Men linkt de oplossing aan de rekenregels van machtverheffing en logaritme

Mirte
3de graad ASO - woensdag 8 juli 2020

Antwoord

Hallo Mirte,

Bedenk:
¹/_x² kan je schrijven als x^-2 (zie Rekenregels voor machten), dus:

f(x) = -ln(x^-2)

Volgens de Rekenregels voor logaritmen is dit weer te schrijven als:

Voor x$>$0: f(x) = -(-2·ln(x)) = 2ln(x)
Voor x$<$0: f(x) = -(-2·ln(-x)) = 2ln(-x) (want (-x)²=x²)

f(x)=ln(x) is een standaardfunctie, de bijbehorende grafiek is (d).
f(x)=ln(-x) is dezelfde functie, maar gespiegeld t.o.v. de y-as. De bijbehorende grafiek is (c).

Je kunt ook redeneren:

Voor zeer grote waarden van x (zowel positief als negatief) is ¹/_x² een zeer klein positief getal;
De logaritme van een zeer klein positief getal is sterk negatief;
f(x) is dan sterk positief.

Voor x bijna nul (zowel positief als negatief) is ¹/_x² een sterk positief getal;
De logaritme van een sterk positief getal is sterk positief;
f(x) is dan sterk negatief.

De grafieken (c) en (d) hebben deze kenmerken.

woensdag 8 juli 2020

©2001-2024 WisFaq