WisFaq!

Geneeskunde toelatingsexamen

Beste is er iemand die me zou kunnen helpen met de volgende vraag: wiskunde juli 2017 vraag 1

Dit is de vraag :
In de volgende figuur worden 4 krommen weergegeven.



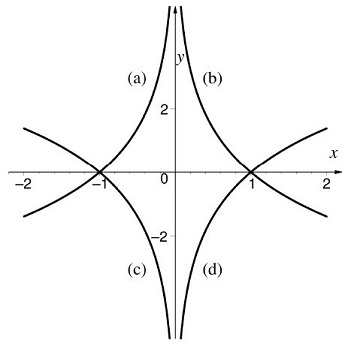
De grafiek van de functie f met functievoorschrift f(x) = -ln(¹/_x²) bestaat uit de unie van welke 2 krommen?

Hoe begin ik hier het best aan om zo snel mogelijk tot een oplossing te komen? Men linkt de oplossing aan de rekenregels van machtverheffing en logaritme

Mirte De Kuyer
8-7-2020

Antwoord

Hallo Mirte,

Bedenk:
¹/_x² kan je schrijven als x^-2 (zie Rekenregels voor machten), dus:

f(x) = -ln(x^-2)

Volgens de Rekenregels voor logaritmen is dit weer te schrijven als:

Voor x$>$0: f(x) = -(-2·ln(x)) = 2ln(x)
Voor x$<$0: f(x) = -(-2·ln(-x)) = 2ln(-x) (want (-x)²=x²)

f(x)=ln(x) is een standaardfunctie, de bijbehorende grafiek is (d).
f(x)=ln(-x) is dezelfde functie, maar gespiegeld t.o.v. de y-as. De bijbehorende grafiek is (c).

Je kunt ook redeneren:

Voor zeer grote waarden van x (zowel positief als negatief) is ¹/_x² een zeer klein positief getal;
De logaritme van een zeer klein positief getal is sterk negatief;
f(x) is dan sterk positief.

Voor x bijna nul (zowel positief als negatief) is ¹/_x² een sterk positief getal;
De logaritme van een sterk positief getal is sterk positief;
f(x) is dan sterk negatief.

De grafieken (c) en (d) hebben deze kenmerken.

GHvD
8-7-2020