
Snelheidsfunctie
Hallo
Ik wil de de maximale verplaatsing berekenen onder een functie. Het gaat gaat om een versnelling tot tijdstip 1/3 t een constante snelheid tot 2/3 t en een vertraging tot snelheid 0 op tmax.
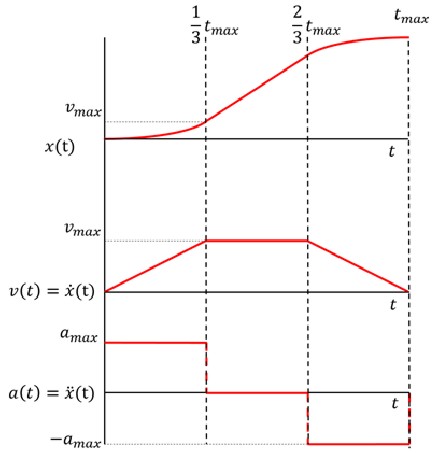
Ik dien xmax te berekenen. Nu is integreren al weer 3 jaar geleden en het lukt me niet goed meer.
Ik snap niet hoe ik aan onderstaande waardes in het rood kom!
Ik weet dat onderstaand goed is, maar wil het zelf ook weer begrijpen.
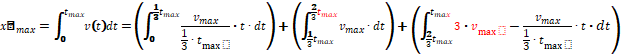 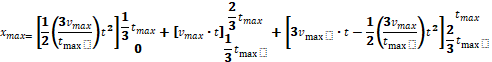
Met vriendelijke groet
michel
Student hbo - maandag 12 februari 2018
Antwoord
Hallo Michel,
Wat betreft de bovengrens 2/3tmax in je tweede integraal: de constante snelheid vmax wordt aangehouden vanaf t=1/3tmax tot t=2/3tmax. De afgelegde weg in dit interval bereken je door de snelheid over de tijd te integreren tussen deze twee tijdstippen, dus ook van 1/3tmax tot 2/3tmax.
Dan de te integreren functie bij de derde integraal: het dalende rode lijnstuk tussen t=2/3tmax tot t=tmax is een deel van een rechte lijn, zie deze figuur:
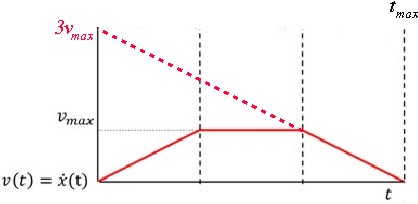
De algemene vergelijking van een rechte lijn is:
v = b + a·t
De waarde b is de y-coördinaat van het snijpunt met de verticale as. In de figuur zie je dat geldt:
b = 3·vmax
De afgelegde weg in het derde tijdsinterval vind je weer door deze functie te integreren van t=2/3tmax tot t=tmax.

dinsdag 13 februari 2018
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|