
Bisectiemethode
Hoe pas ik de bisectiemethode toe op deze functie: ex=3x voor een x die tussen het interval(0,1) ligt?
Jan
Student universiteit BelgiŽ - dinsdag 12 augustus 2014
Antwoord
Definieer de functie $F(x)=e^x-3x$. We gaan op zoek naar $\alpha$ zodat $F(\alpha)=0$.
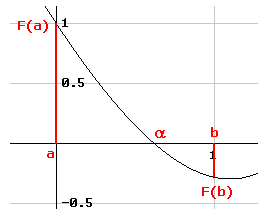
$F$ is continu op $[0,1]$ en $F(0)\times F(1)\lt0$. Er is minstens één nulpunt en we veronderstellen dat er ook hoogstens één nulpunt is.
Je berekent dan $m$ = $\large\frac{a+b}{2}$ en berekent $F(m)$.
Er zijn dan drie mogelijkheden:
-
Als $F(m)=0$ dan hebben we $\alpha$ gevonden en zijn we dus klaar.
-
Als $F(a)\times F(m)\lt0$ dan neem $b=m$ en herhaal het proces.
-
Als $F(a)\times F(m)\gt0$ dan neem $a=m$ en herhaal het proces
We stoppen als $|a-b|\lt\epsilon$
Dat ziet er dan zo uit:
We noemen dit de halveringsmethode of bisectiemethode...
Naschrift
|
n
|
a
|
b
|
m
|
F(m)
|
F(a)xF(m)
|
|
0
|
0
|
1
|
0,5
|
0,148721271
|
0,148721271
|
|
1
|
0,5
|
1
|
0,75
|
-0,132999983
|
-0,019779927
|
|
2
|
0,5
|
0,75
|
0,625
|
-0,006754043
|
-0,00100447
|
|
3
|
0,5
|
0,625
|
0,5625
|
0,067554657
|
0,010046814
|
|
4
|
0,5625
|
0,625
|
0,59375
|
0,029516072
|
0,001993948
|
|
5
|
0,59375
|
0,625
|
0,609375
|
0,011156489
|
0,000329296
|
|
6
|
0,609375
|
0,625
|
0,6171875
|
0,002144652
|
2,39268E-05
|
|
7
|
0,6171875
|
0,625
|
0,62109375
|
-0,002318893
|
-4,97322E-06
|
|
8
|
0,6171875
|
0,62109375
|
0,619140625
|
-9,06632E-05
|
-1,94441E-07
|
|
9
|
0,6171875
|
0,619140625
|
0,618164063
|
0,00102611
|
2,20065E-06
|
|
10
|
0,618164063
|
0,619140625
|
0,618652344
|
0,000467502
|
4,79708E-07
|
|
11
|
0,618652344
|
0,619140625
|
0,618896484
|
0,000188364
|
8,80605E-08
|
|
12
|
0,618896484
|
0,619140625
|
0,619018555
|
4,88366E-05
|
9,19905E-09
|
|
13
|
0,619018555
|
0,619140625
|
0,61907959
|
-2,09168E-05
|
-1,0215E-09
|
|
14
|
0,619018555
|
0,61907959
|
0,619049072
|
1,3959E-05
|
6,81711E-10
|
|
15
|
0,619049072
|
0,61907959
|
0,619064331
|
-3,47909E-06
|
-4,85647E-11
|
|
16
|
0,619049072
|
0,619064331
|
0,619056702
|
5,23992E-06
|
7,31442E-11
|
|
17
|
0,619056702
|
0,619064331
|
0,619060516
|
8,80402E-07
|
4,61323E-12
|
|
18
|
0,619060516
|
0,619064331
|
0,619062424
|
-1,29935E-06
|
-1,14395E-12
|
|
19
|
0,619060516
|
0,619062424
|
0,61906147
|
-2,09473E-07
|
-1,84421E-13
|
|
20
|
0,619060516
|
0,61906147
|
0,619060993
|
3,35464E-07
|
2,95343E-13
|
Na 20 'slagen' hebben we gevonden $x\approx0,619060993$. Derive geeft als benadering $x\approx0,6190612867$, dus 't schiet al lekker op.

dinsdag 12 augustus 2014
 ©2001-2025 WisFaq
©2001-2025 WisFaq
|