Re: Bewijs driehoek gelijkbenig cirkels

Dit is een reactie op vraag 67235

Kan het ook met de stelling van Pythagoras?

Daaf S
Iets anders - dinsdag 27 maart 2012

Antwoord

Dag Daaf,
Jazeker. En bedankt voor je vraag!

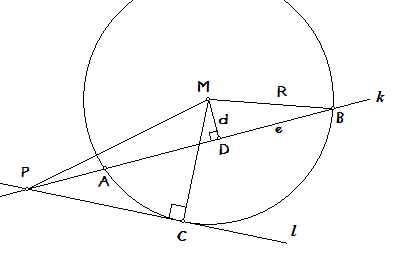
Teken de lijnstukken MP, MB, MC en ook MD, waarbij D het midden is van het lijnstuk AB.
Met MD = d, BD = e (= AD) en met R als lengte van de straal van de cirkel geldt:
- PM² = PC² + R² (in driehoek PMC)
- PM² = PD² + d² (in driehoek PMD)
- d² = R² - e² (in driehoek BMD)
Uit deze drie relaties volgt dan:
PC² + R² = PD² + (R² - e²)
Zodat:
PC² = PD² - e² = (PD - e)(PD + e)
Of:
PC² = PA · PB

dinsdag 27 maart 2012

Re: Re: Bewijs driehoek gelijkbenig cirkels

©2001-2024 WisFaq