Vierkant en driehoeken
Hallo Wisfaq,
Het lukt me niet een plaatje te maken maar ik probeer het zo.
Een vierkant ABCD met zijde x wordt aan de bovenzijde in 2 gelijke delen(x/2) gedeeld.Van daaruit teken ik een rechthoekige driehoek met rechte hoek op het punt waar de halve zijde bovenaan zich bevindt .Hoek F =90° Trek nu FB uit dit punt F naar het punt B op het vierkant onderaan rechts en FE naar de zijde van het vierkant op de linkerzijde . Bereken nu de hoek gelegen onder hoek E en aansluitend op de linkerzijde van het vierkant.
Oef....
Groetjes en dank voor je antwoord alvast nu !!
Rik
Rik Le
Iets anders - woensdag 20 oktober 2010
Antwoord
Hoi Rik,
Ik verwacht, dat je onderstaande tekening zo'n beetje bedoeld:
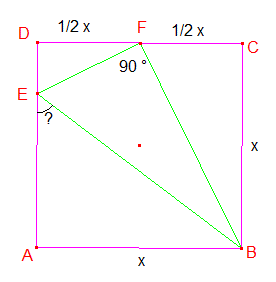
ÐBFE=90 graden
Dus: ÐEFD + ÐBFC = 90 graden
(gebruik gemaakt van: gestrekte hoek van 180 graden)
In DBCF geldt:
ÐFBC + ÐBFC = 90 graden
Dus: ÐEFD = ÐFBC
Conclusie: DEFD~DFBC (gelijkvormig)
BC/FD=FC/ED
x/1/2x=1/2x/ED
ED=1/4x
Dan AE=3/4x
Kijk nu in DABE:
tan(ÐAEB)=x/3/4x=4/3
ÐABE=tan-1(4/3) 53°
Hopelijk volg je mijn denkstappen. Denk er waal aan dat dit één manier is, er zijn nog andere volgroutes om de som op te lossen.
Mvg Thijs Bouten
donderdag 21 oktober 2010
©2001-2024 WisFaq
|
Re: Vierkant en driehoeken