WisFaq!

Vierkant en driehoeken

Hallo Wisfaq,
Het lukt me niet een plaatje te maken maar ik probeer het zo.
Een vierkant ABCD met zijde x wordt aan de bovenzijde in 2 gelijke delen(x/2) gedeeld.Van daaruit teken ik een rechthoekige driehoek met rechte hoek op het punt waar de halve zijde bovenaan zich bevindt .Hoek F =90° Trek nu FB uit dit punt F naar het punt B op het vierkant onderaan rechts en FE naar de zijde van het vierkant op de linkerzijde . Bereken nu de hoek gelegen onder hoek E en aansluitend op de linkerzijde van het vierkant.
Oef....
Groetjes en dank voor je antwoord alvast nu !!
Rik

Rik Lemmens
20-10-2010

Antwoord

Hoi Rik,

Ik verwacht, dat je onderstaande tekening zo'n beetje bedoeld:


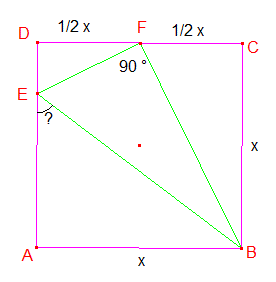
ÐBFE=90 graden
Dus: ÐEFD + ÐBFC = 90 graden
(gebruik gemaakt van: gestrekte hoek van 180 graden)

In DBCF geldt:
ÐFBC + ÐBFC = 90 graden

Dus: ÐEFD = ÐFBC

Conclusie: DEFD~DFBC (gelijkvormig)

^BC/_FD=^FC/_ED
^x/_¹/2x=^1/₂x/_ED
ED=¹/₄x

Dan AE=³/₄x

Kijk nu in DABE:

tan(ÐAEB)=^x/_³/4x=⁴/₃
ÐABE=tan^-1(⁴/₃)53°

Hopelijk volg je mijn denkstappen. Denk er waal aan dat dit één manier is, er zijn nog andere volgroutes om de som op te lossen.

Mvg Thijs Bouten

tb
21-10-2010