Omwentelingslichaam van 2 driehoeken

Bewijs dat de inhoud van het lichaam ontstaan door het wentelen van de twee rechthoekige driehoeken rond de gemeenschappelijke rechthoekzijde gelijk is aan;

1/3 h (pi.R² + pi.r² - pi.R.r)

ps. de twee driehoeken staan met hun punt op elkaar

wim
2de graad ASO - zondag 15 december 2002

Antwoord

Eerst maar eens een tekening:



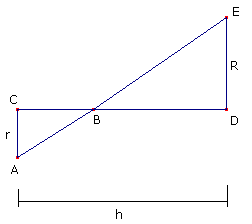
Als je deze figuur draait om de lijn CD krijg je een lichaam dat bestaat uit twee kegels. De vraag is dan: wat is de inhoud van dat lichaam?

Laten we BD maar eens p noemen, dan is BC=h-p.

De inhouden:
I_groot=¹/₃pR²·p
I_klein=¹/₃pr²·(h-p)

I_totaal=¹/₃pR²·p+¹/₃pr²·(h-p)
I_totaal=¹/₃pR²·p+¹/₃pr²·h-¹/₃pr²·p

Nou moeten we die p nog zien kwijt te raken!
Er geldt (ik ga er van uit dat de twee driehoeken gelijkvormig zijn!):



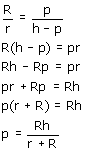
En als je dit dan invult in bovenstaande uitdrukking dan krijg je zoiets als:

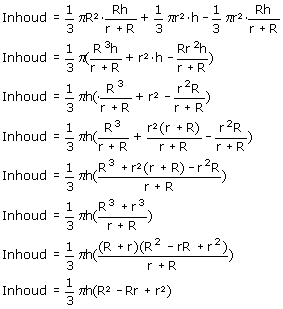
zondag 15 december 2002

©2001-2024 WisFaq